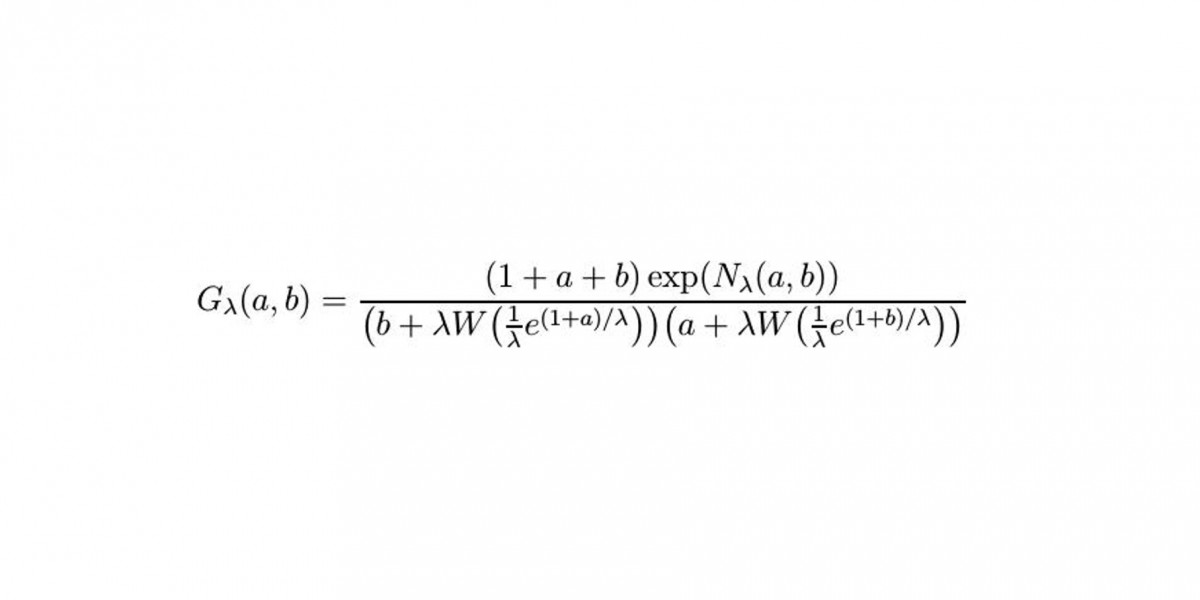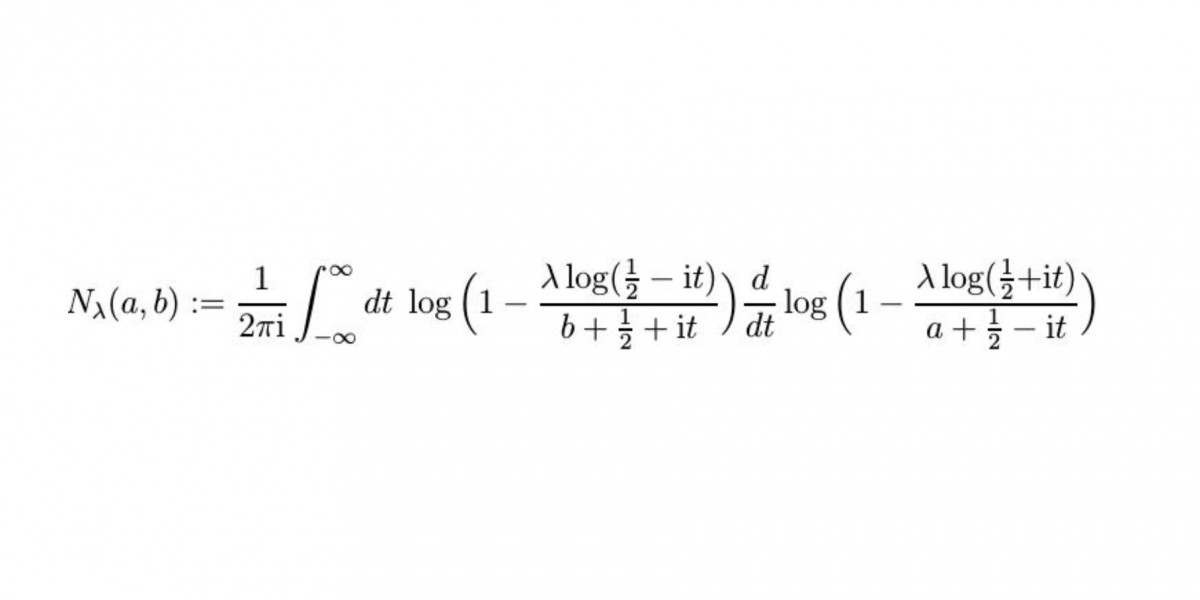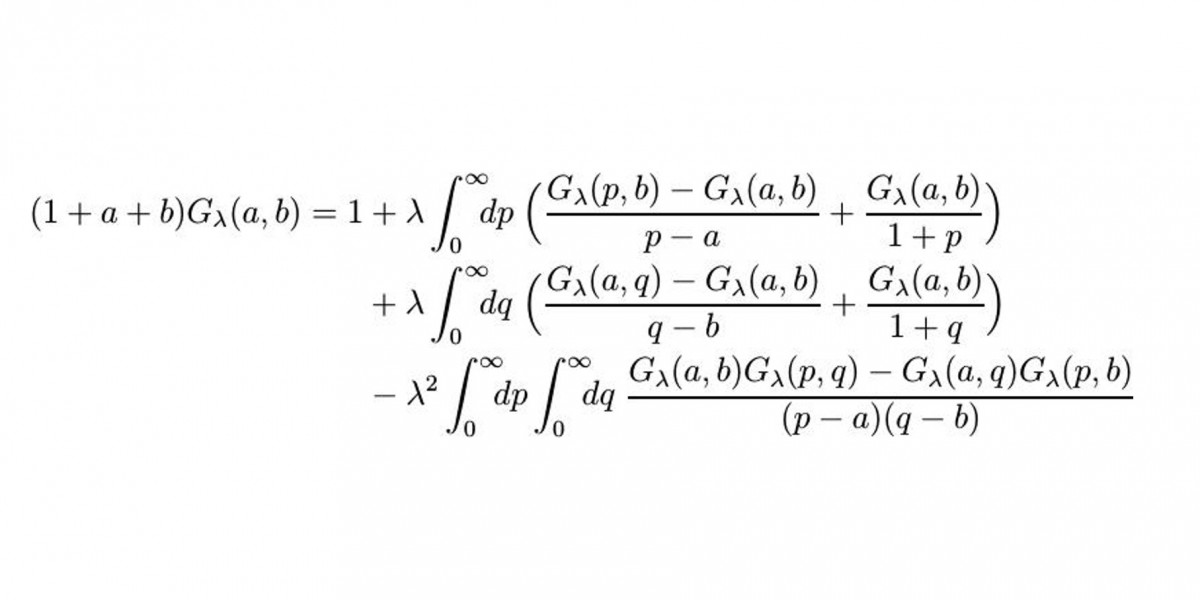
"Ich dachte: So viel Glück kann man doch gar nicht haben"
Es hat rund zehn Jahre gedauert, aber dann kam der große Moment: Prof. Dr. Raimar Wulkenhaar vom Mathematischen Institut der Westfälischen Wilhelms-Universität Münster (WWU) und seinem Kollegen Dr. Erik Panzer von der Universität Oxford ist es gelungen, eine mathematische Gleichung zu lösen, die als unlösbar galt. Die Gleichung soll eingesetzt werden, um Fragen der Elementarteilchen-Physik zu beantworten. Im Interview mit Christina Heimken erinnert sich Raimar Wulkenhaar an die Herausforderungen bei der Suche nach der Lösungsformel und erklärt, warum die Arbeit noch nicht abgeschlossen ist.
Sie haben zehn Jahre an der Lösung der Gleichung gearbeitet. Was macht diese Gleichung so schwer lösbar?
Es handelt sich um eine nichtlineare Integralgleichung mit zwei Variablen. Solch eine Gleichung ist so komplex, dass man eigentlich denkt, es kann keine Lösungsformel geben. Zwei Variablen sind für sich genommen schon eine Herausforderung. Da gibt es für nichtlineare Integralgleichungen keine etablierten Lösungsansätze. Jedoch gab es in den zehn Jahren immer wieder Lichtblicke, sodass mir trotz aller Schwierigkeiten eine explizite Lösungsformel, ausgedrückt durch bekannte Funktionen, möglich schien.
Wofür kann man die Gleichung nutzen?
Es geht um ein mathematisches Verständnis von Quantenfeldtheorien. Diese gehören in den Bereich der Physik und spielen bei großen Experimenten wie beispielsweise am CERN eine Rolle. Ziel ist es, Elementarteilchen, also die kleinsten bekannten Bausteine der Materie, mathematisch zu beschreiben. Das ist allerdings derart kompliziert, dass man stattdessen gedachte Teilchen mathematisch beschreibt, die bestimmte Eigenschaften der realen Teilchen enthalten. Die Hoffnung ist, mit den auf diese Weise etablierten Methoden irgendwann die realen Teilchen beschreiben zu können.

Ende Mai probierte ich eine Idee aus, für die mein Doktorand Alexander Hock den entscheidenden Anstoß gegeben hatte. Ich erarbeitete eine neue Gleichung, einfacher als die bisherige, und begann, diese in Schleifen zu lösen. Das bedeutet: Man nähert sich der Lösung Schritt für Schritt – also Schleife für Schleife – an, indem die im jeweils letzten Schritt ausgerechnete linke Seite der Gleichung für den nächsten Schritt in die rechte Seite eingesetzt wird. In der vierten Schleife musste ich eine Summe aus 46 Integralen berechnen, die unter anderem Polylogarithmen enthielten. Diese Polylogarithmen, die zu den anspruchsvolleren Funktionen gehören, wurden in jeder Schleife komplizierter. Mein Glück: Aufsummiert kürzte sich fast alles weg, und es blieb nur eine kurze Summe aus Potenzen gewöhnlicher Logarithmen übrig. Mir war sofort klar, dass hier ein Schatz liegt ...
... womit das Problem gelöst war?
Nein, denn die fünfte Schleife war nicht so leicht lösbar. Doch ich hatte wieder Glück. Bei einer Sommerschule in den französischen Alpen hatte ich die Gelegenheit, mich mit Experten für solche Funktionen auszutauschen. Dr. Erik Panzer von der Universität Oxford hat beispielsweise ein Computerprogramm zur symbolischen Mathematik von Hyperlogarithmen geschrieben und mich unterstützt. Über Nacht hat dieses Programm meine Gleichung bis zur siebten Schleife ausgerechnet. Es hat meine Ergebnisse bis zur vierten Schleife bestätigt, und nach der vierten Schleife ging das Wunder weiter: Alles ließ sich auf gewöhnliche Logarithmen herunterbrechen. Es zeichnete sich ein Muster ab!
Was bedeutet das?
Vielleicht erinnern Sie sich aus Schulzeiten noch an das Pascalsche Dreieck, das die Binominalkoeffizienten enthält. Dabei ist jeder Eintrag in einer Zeile des Dreiecks die Summe der zwei darüberstehenden Einträge. Solch eine dreieckige Struktur, wenn auch komplizierter als beim Pascalschen Dreieck, finden wir in unseren Schleifen. Am 9. Juni waren die Schleifen acht und neun fertig. Und dann kam der vielleicht wichtigste Moment: Erik Panzer entzifferte eine sogenannte Rekursionsformel, die die jeweils letzte Zeile des Dreiecks aus der darüberliegenden Zeile generiert, mit der man also vom Bekannten auf das Unbekannte schließen kann.
Was ging Ihnen in diesem Moment durch den Kopf?
Unter anderem dachte ich: So viel Glück kann man doch gar nicht haben. Mir war klar: Wir werden die Gleichung lösen. Beim Abendessen gab es eine Flasche Wein für unseren Tisch ...
… bevor Sie sich wieder an die Arbeit machten.
Ja. Mir gelang es am nächsten Tag, einen Teil der Gleichung auf eine einfache Reihe von Ableitungen zu reduzieren. Der Rest erschien zunächst schwierig. Erst am späten Abend hatte ich die Idee, die Cauchy-Formel zur Lösung zu nutzen. Ich stellte den Wecker für den nächsten Morgen auf 5:30 Uhr und probierte es direkt aus. Es funktionierte auf Anhieb, und im nächsten Schritt stieß ich auf eine Formel, die mir schon häufig begegnet war. Ich wusste, sie wird durch die Lambert-W-Funktion gelöst. Wenige Minuten später erhielt ich eine E-Mail von Erik Panzer: Auch er kam auf die Lambert-Funktion, und das auf völlig anderem Weg. In fünf Tagen war uns damit gelungen, was in zehn Jahren zuvor nicht zu schaffen gewesen war: die Lösung jener Integralgleichung, die das Modell einer Quantenfeldtheorie beschreibt. Das war einfach unglaublich.
Sie nutzen Ideen und Techniken, die Mathematiker im 18. Jahrhundert entwickelten, die aber inzwischen fast vergessen sind.
Diese alten Formeln haben uns sehr geholfen. Die Lambert-W-Funktion, die ein elementarer Teil unserer Lösung ist, ist nach dem Schweizer Mathematiker Johann Heinrich Lambert benannt. Diese Gleichung tritt in sehr vielen und völlig verschiedenen Fragestellungen auf. In Unkenntnis der Vorarbeiten wurde die Lambert-Funktion allerdings immer wieder neu erfunden und erst 1993 als Standard etabliert. Außerdem nutzten wir die Lagrange-Bürmann-Formel, die uns half, ein Integral über die Lambert-Funktion aufzulösen, und die Cauchy-Formel. Die Mathematik geht generell sehr respektvoll mit ihren Vorfahren um. Namen wie Euler, Lambert, Lagrange, Cauchy, Gauß und Hilbert zitiert man in größter Anerkennung. Es gibt aber auch zwei neuere Werkzeuge, die ich nicht missen möchte: Wikipedia und Computer-Algebra. Bei Wikipedia findet man umfassende Informationen zu bekannten und weniger bekannten mathematischen Strukturen und Funktionen. Computer können Gleichungen ungleich schneller und fehlerfreier lösen, als es per Hand möglich ist.
Wie geht es jetzt weiter?
In unserer Lösung taucht eine neue Funktion auf, die wir Nielsen-Funktion genannt haben. Wenn wir sie besser verstehen und beispielsweise klären, wie sie mit anderen bekannten Funktionen zusammenhängt, werden wir unsere Arbeit, die als Vorabdruck online frei zugänglich ist, bei einer Fachzeitschrift mit Peer-Review-Verfahren zur Veröffentlichung einreichen. Anschließend möchte ich Arbeiten weiterführen, die ich seit 2002 mit meinem Kollegen Prof. Dr. Harald Grosse aus Wien verfolge. Es betrifft eine Quantenfeldtheorie für mathematische Teilchen. Dieses Modell werden wir nun mithilfe der gelösten Gleichung vollständig verstehen.