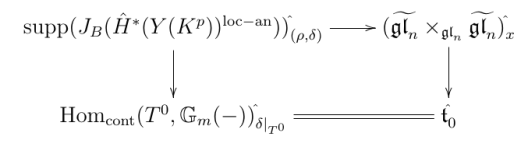Arithmetic and Groups

© MM

Research Area A

Bays (until 2023), Cuntz, Deninger, Gardam (2022-2023), Hartl, Hellmann, Hille, Hils, Jahnke, Kwiatkoswka, Lourenço (since 2024), Nikolaus, Scherotzke (until 2020), R. Schindler, Schlutzenberg (until 2023), Schneider, Scholbach (until 2022), Schürmann, Tent, Viehmann (since 2022), Zhao (since 2024).

Research Area A will focus on problems of algebraic nature with methods ranging from representation and cohomology theory to model theory and mathematical logic. The p-adic and characteristic p Langlands correspondences that relate arithmetic invariants with automorphic representations are major research topics. We also aim at developing new powerful cohomology theories in algebra and arithmetic geometry. One of the long-term goals is to understand Hasse-Weil zeta functions cohomologically.

In group theory, we plan to develop new techniques for small cancellation theory in order to construct sharply 2-transitive groups in sufficiently large finite characteristic. On the model theoretic side, the focus will be on understanding and classifying NIP groups and fields as well as on classifying and constructing ample strongly minimal structures. In set theory and descriptive set theory, we will be studying Varsovian models as well as Polish group actions.

  • A1. Arithmetic, geometry and representations.

    The Langlands programme relates representations of (the adele valued points of) reductive groups G over Q - so-called automorphic representations - with certain representations of the absolute Galois group of Q. This programme includes the study of these objects over general global fields (finite extension of Q or Fp (t)) and local fields as well. In its local form the classical programme only considered l-adic Galois representations of p-adic fields for unequal primes l neq p. In order to allow for a p-adic variation of the objects, it is absolutely crucial to extend it to the case l = p. In the global situation, the automorphic representations in question can often be realised in (or studied via) the cohomology of a tower of Shimura varieties (or related moduli spaces) attached to the group G.

    We will focus on the following directions within this programme:
    The p-adic and mod p Langlands programme asks for an extension of such a correspondence involving certain continuous representations with p-adic respectively mod p coefficients. Broadening the perspective to p-adic automorphic forms should, for example, enable us to capture all Galois representations, not just those having a particular Hodge theoretic behaviour at primes dividing p. This extended programme requires the introduction of derived categories. We will study differential graded Hecke algebras and their derived categories on the reductive group side. On the Galois side, we hope to use derived versions of the moduli spaces of p-adic Galois representations introduced by Emerton and Gee.

    The geometric Langlands programme is a categorification of the Langlands programme. We plan to unify the different approaches using motivic methods.
    In another direction, we study the geometry and arithmetic of moduli stacks of global G-shtukas over function fields. Their cohomology has been the crucial tool to establish large parts of the local and global Langlands programme over function fields. Variants of G-shtukas are also used to construct and investigate families of p-adic Galois representations.

    Cohomology theories are a universal tool pervading large parts of algebraic and arithmetic geometry. We will develop and study cohomology theories, especially in mixed characteristic, that generalise and unify étale cohomology, crystalline cohomology and de Rham cohomology as well as Hochschild cohomology in the non-commutative setting. Developing (topological) cyclic homology in new contexts is an important aim. A main goal is to construct a cohomology theory that can serve the same purposes for arithmetic schemes as the l-adic or crystalline cohomology with their Frobenius actions for varieties over finite fields. Ideas from algebraic geometry, algebraic topology, operator algebras and analysis blend in these investigations.

  • A2. Groups, model theory and sets.

    Model theory and, more generally, mathematical logic as a whole has seen striking applications to arithmetic geometry, topological dynamics and group theory. Such applications as well as fundamental questions in geometric group theory, on the foundations of model theory and in set theory are at the focus of our work.
    The research in our group reaches from group theoretic questions to the model theory of groups and valued fields as well as set theory. The study of automorphism groups of first order structures as topological groups, for examples, uses tools from descriptive set theory leading to pure set theoretic questions.

     

Further research projects of Research Area A members

• CRC 1442 - A04: New cohomology theories for arithmetic schemes

The goal of this project is to study cohomology theories for schemes in order to attack important open problems in arithmetic. Among these theories are topological periodic homology (TP), topological cyclic homology (TC), rational de Rham–Witt cohomology, prismatic cohomology, K-theory, L-Theory and leafwise cohomology of associated dynamical systems. We will prove structural results about those theories as well as make further calculations of specific cases.

online
Project members: Christopher Deninger, Thomas Nikolaus

• CRC 1442 - D03: Integrability

We investigate blobbed topological recursion for the general Kontsevich matrix model, as well as the behaviour of Baker–Akhiezer spinor kernels for deformations of the spectral curve and for the quartic Kontsevich model. We study relations between spin structures and square roots of Strebel differentials, respectively between topological recursion and free probability. We examine factorisation super-line bundles on infinite-dimensional Grassmannians and motivic characteristic classes for intersection cohomology sheaves of Schubert varieties.

online
Project members: Jörg Schürmann, Raimar Wulkenhaar, Yifei Zhao

• CRC 1442 - C04: Group theoretic aspects of negative curvature

We will continue to investigate iterated small cancellation groups. We recently gave a relatively short proof of the infinity of the free Burnside groups of sufficiently large odd exponent which is based on a few important principles well-studied in hyperbolic groups. In a next step we will develop a meta theorem based on these principles which will be applicable to a wider range of problems, in particular in the context of sharply multiply transitive groups. We will also study complexes associated to hyperbolic groups from a model theoretic perspective.

online
Project members: Katrin Tent

• CRC 1442 - A01: Automorphic forms and the p-adic Langlands programme

The past years have seen tremendous progress in the development of a categorical approach to the arithmetic of the Langlands programme. In the context of the p-adic Langlands programme the main features of this approach are the study of derived categories of p-adic representations of p-adic Lie groups, the study of (coherent) sheaves on moduli of Galois representations associated to such representations, and the development of a more geometric approach to such representations. The project addresses all these three aspects of the programme.

online
Project members: Peter Schneider, Eugen Hellmann

• CRC 1442 - A02: Moduli spaces of p-adic Galois representations

Representations of the absolute Galois group of a p-adic local field with p-adic coefficients are studied most fruitfully in terms of semi-linear algebra objects called (phi,Gamma)-modules. In part of the project we will advance the study of (phi,Gamma)-modules. In another part we use (phi,Gamma)-modules to construct and study moduli spaces of Galois representation that occur in the context of the p-adic Langlands programme.

online
Project members: Peter Schneider, Eugen Hellmann

• CRC 1442 - Z01: Central Task of the Collaborative Research Centre online
Project members: Eugen Hellmann

• CRC 1442: Geometry: Deformation and Rigidity

From its historic roots, geometry has evolved into a cornerstone in modern mathematics, both as a tool and as a subject in its own right. On the one hand many of the most important open questions in mathematics are of geometric origin, asking for example to what extent an object is determined by geometric properties. On the other hand, abstract mathematical problems can often be solved by associating them to more geometric objects that can then be investigated using geometric tools. A geometric point of view on an abstract mathematical problem quite often opens a path to its solution.Deformations and rigidity are two antagonistic geometric concepts which can be applied in many abstract situations making transfer of methods particularly fruitful. Deformations of mathematical objects can be viewed as continuous families of such objects, like for instance evolutions of a shape or a system with time. The collection of all possible deformations of a mathematical object can often be considered as a deformation space (or moduli space), thus becoming a geometric object in its own right. The geometric properties of this space in turn shed light on the deeper structure of the given mathematical objects. We think of properties or of quantities associated with mathematical objects as rigid if they are preserved under all (reasonable) deformations.A rigidity phenomenon refers to a situation where essentially no deformations are possible.Rigidity then implies that objects which are approximately the same must in fact be equal, making such results important for classifications.The overall objective of our research programme can be summarised as follows:Develop geometry as a subject and as a powerful tool in theoretical mathematics focusing on the dichotomy of deformations versus rigidity. Use this unifying perspective to transfer deep methods and insights between different mathematical subjects to obtain scientific breakthroughs, for example concerning the Langlands programme, positive curvature manifolds, K-theory, group theory, and C*-algebras.

online
Project members: Eugen Hellmann

• CRC 1442 - C02: Homological algebra for stable ∞-categories

The general goal of the project is to study the homological algebra of stable infinity-categories and Poincaré infinity-categories. This is done through the theory of non-commutative motives and Efimov K-Theory. Concrete goals are to give a new approach to controlled algebra (thereby attacking open problems and conjectures in geometric topology) and obtain new structural results about the category of motives. The latter thus yields new results about K-Theory and TC, e.g. we try to resolve the long-standing open question about a universal property for TC.

online
Project members: Thomas Nikolaus

• CRC 1442 - A05: Moduli spaces of local shtukas in mixed characteristic

We study the geometry and cohomology of moduli spaces of local G-shtukas, a class of moduli spaces that plays a central role in the geometrisation of Langlands correspondences. More precisely, we are interested in the geometry of the image of the period maps, want to investigate étale sheaves on the moduli spaces and aim at the local Langlands correspondence for covering groups via a metaplectic geometric Satake equivalence.

online
Project members: Yifei Zhao, Eva Viehmann

• Model Theory of Valued Fields with Endomorphism

We propose a model-theoretic investigation of valued fields with non-surjective endomorphism. The model theory of valued fields with automorphism, in particular the Witt Frobenius case treated by Bélair, Macintyre and Scanlon, was extensively developed over the last 15 years, e.g., obtaining Ax-Kochen-Ershov principles for various classes of σ-henselian valued difference fields. We plan to generalize these results to the non-surjective context. The most natural example of a non-surjective endomorphism is the Frobenius map on an imperfect field. In analogy to the Witt Frobenius, the main examples for our study are Cohen fields over imperfect residue fields endowed with a lift of the Frobenius. The model theory of Cohen fields was recently developed in the work of Anscombe and Jahnke. In order to obtain Ax-Kochen-Ershov type results in our setting, it will be necessary to firstunderstand the equicharacteristic 0 case. This case is interesting in its own right, as it encompasses the asymptotic theory of Cohen fields with Frobenius lift. We are particularly interested in obtaining relative completeness and transfer of model theoretic tameness notions from value group and residue field to the valued difference field, as well as in identifying model companions for various subclasses. In all these cases, the endomorphism is an isometry of the valued field.
Another natural example of a σ-henselian valued difference fields is given by ultraproducts ofseparably closed valued fields with Frobenius. Here, the endomorphism is no longer an isometry, and the induced automorphism of the value group is ω-increasing. By work of Chatzidakis and Hrushovski the residue difference field of such an ultraproduct is existentially closed as a field with distinguished endomorphism. We aim to show the analogous result for the valued difference field, namely that it is existentially closed in a natural language, and infer existence and an axiomatization of the model-companion from this.
online
Project members: Franziska Jahnke, Martin Hils

• Geometry and Arithmetic of Uniformized Structures online
Project members: Eva Viehmann

• Geometric and Combinatorial Configurations in Model Theory Model theory studies structures from the point of view of first-order logic. It isolates combinatorial properties of definable sets and uses these to obtain algebraic consequences. A key example is the group configuration theorem, a powerful tool in geometric stability used, e.g., to prove the trichotomy for Zariski geometries and in recent applications to combinatorics. Valued fields are an example of the confluence of stability theory and algebraic model theory. While Robinson studied algebraically closed valued fields already in 1959, the tools from geometric stability were only made available in this context in work of Haskell-Hrushovski-Macpherson, brought to bear in Hrushovski-Loeser's approach to non-archimedean geometry. In the project, we aim to strengthen the recent relations between model theory and combinatorics, develop the model theory of valued fields using tools from geometric stability and carry out an abstract study of the configurations which are a fundamental tool in these two areas. online
Project members: Katrin Tent, Franziska Jahnke, Martin Hils