Research
The aim of research at Mathematics Münster is the implementation of integrated approaches to solve important problems across different mathematical fields. We view mathematical research as an organic whole with countless connections between fields, and specifically promote the development of mathematical methods that lead to cross-disciplinary scientific breakthroughs.
Guided by the three unifying principles Dynamics–Geometry–Structure, we thoroughly analyse how mathematical objects dynamically evolve, consistently adopt a geometric perspective, and identify deeper, often hidden structures behind specific problems.
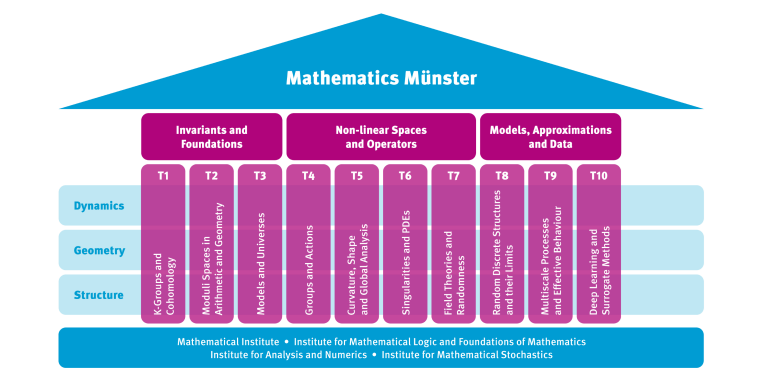
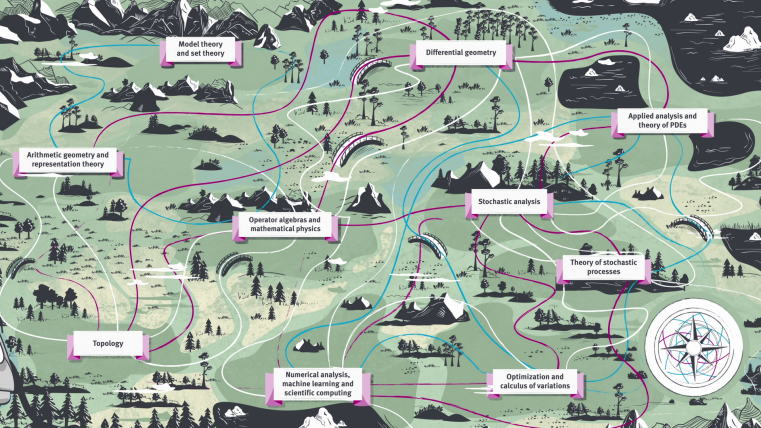
Mathematical fields
- Model theory and set theory
- Arithmetic geometry and representation theory
- Topology
- Operator algebras and mathematical physics
- Differential geometry
- Analysis of partial differential equations
- Stochastic analysis
- Theory of stochastic processes
- Optimisation and calculus of variations
- Numerical analysis, machine learning and scientific computing
Research examples
Browse through the posters!
K-theory via Prismatic Cohomology© MM/Nikolaus 
Moduli of Galois representations© MM/Hellmann 
From algebraicity conjectures to geometric group theory© MM/Tent 
From forcing axioms to the stars© MM/Schindler 
Hopf conjencture© MM/Wilking, Wiemeler 
Singular SPDEs© MM/Weber 
Dilute Curie-Weiss models© MM/Löwe, Kabluchko 
Randomly perforated media© MM/Zippieri 
Multiscale fluid flow© MM/ Engwer, Seis 
Nonlinear model order reduction (MOR)© MM/Ohlberger
Latest research news
Mini-course "Stochastic PDEs and Scaling Limits" available now
Talk series by Hendrik Weber at SLMath
Excellence confirmed: "Mathematics Münster" receives continued funding
