Forschung
Das Ziel der Forschung in Mathematik Münster (MM) ist die Umsetzung integrierter Ansätze zur Lösung grundlegender Probleme in verschiedenen mathematischen Bereichen. Wir betrachten die mathematische Forschung als ein organisches Ganzes mit unzähligen Verbindungen zwischen den Gebieten und fördern gezielt die Entwicklung mathematischer Methoden, die zu disziplinübergreifenden wissenschaftlichen Durchbrüchen führen.
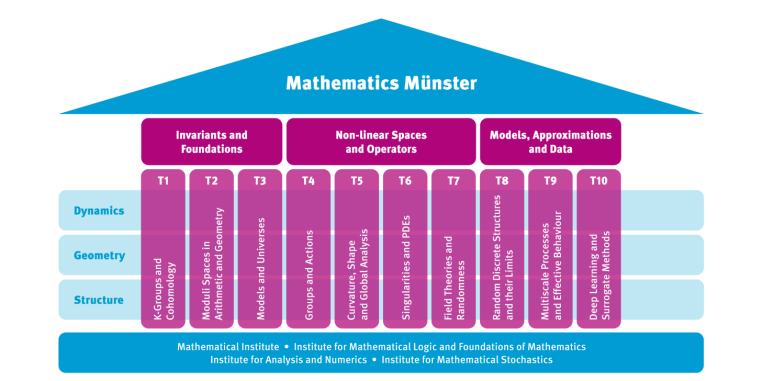
Geleitet von den drei Prinzipien Dynamik–Geometrie–Struktur analysieren wir die dynamische Entwicklung mathematischer Objekte, nehmen konsequent eine geometrische Perspektive ein und identifizieren die tieferen, oft verborgenen Strukturen hinter Problemen.
Da sich die Inhalte dieser Seite an eine internationale Forschungsgemeinschaft richten, sind diese überwiegend auf den englischsprachigen Seiten zu finden.
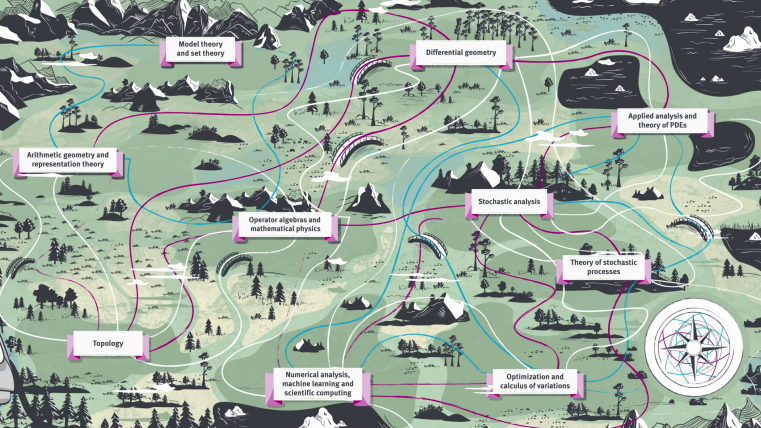
Mathematische Felder
- Model theory and set theory
- Arithmetic geometry and representation theory
- Topology
- Operator algebras and mathematical physics
- Differential geometry
- Analysis of partial differential equations
- Stochastic analysis
- Theory of stochastic processes
- Optimisation and calculus of variations
- Numerical analysis, machine learning and scientific computing
Research examples
Schauen Sie sich die Poster an!
K-theory via Prismatic Cohomology© MM/Nikolaus 
Moduli of Galois representations© MM/Hellmann 
From algebraicity conjectures to geometric group theory© MM/Tent 
From forcing axioms to the stars© MM/Schindler 
Hopf conjencture© MM/Wilking, Wiemeler 
Singular SPDEs© MM/Weber 
Dilute Curie-Weiss models© MM/Löwe, Kabluchko 
Randomly perforated media© MM/Zippieri 
Multiscale fluid flow© MM/ Engwer, Seis 
Nonlinear model order reduction (MOR)© MM/Ohlberger
News aus der Forschung
Minikurs "Stochastic PDEs and Scaling Limits" jetzt online verfügbar
Vortragsreihe von Hendrik Weber am SLMath
Exzellenz bestätigt: "Mathematics Münster" wird weiter gefördert
