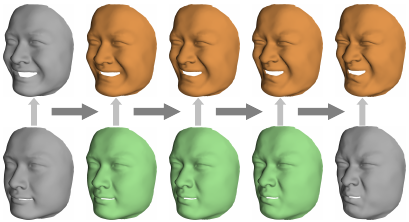
Bezier curves are a widespread tool for the design of curves in Euclidian space. This paper generalizes the notion of Bezier curves to the infinite-dimensional space of images. To this end the space of images is equipped with a Riemannian metric which measures the cost of image transport and intensity variation in the sense of the metamorphosis model [MY01]. Bezier curves are then computed via the Riemannian version of de Casteljau’s algorithm, which is based on a hierarchical scheme of convex combination along geodesic curves. Geodesics are approximated using a variational discretization of the Riemannian path energy. This leads to a generalized de Casteljau method to compute suitable discrete Bezier curves in image space. Selected test cases demonstrate qualitative properties of the approach. Furthermore, a Bezier approach for the modulation of face interpolation and shape animation via image sketches is presented.

We prove both in the smooth and discrete setting that the Hessian of an elastic deformation energy results in a proper Riemannian metric on the space of shells (modulo rigid body motions). Based on this foundation we develop a time- and space-discrete \emph{geodesic calculus}. In particular we show how to shoot geodesics with prescribed initial data, and we give a construction for parallel transport in shell space. This enables, for example, natural extrapolation of paths in shell space and transfer of large nonlinear deformations from one shell to another with applications in animation, geometric, and physical modeling. Finally, we examine some aspects of curvature on shell space.

A new approach for the effective computation of geodesic regression curves in shape spaces is presented. Here, one asks for a geodesic curve on the shape manifold that minimizes a sum of dissimilarity measures between given two- or three-dimensional input shapes and corresponding shapes along the regression curve. The proposed method is based on a variational time discretization of geodesics. Curves in shape space are represented as deformations of suitable reference shapes, which renders the computation of a discrete geodesic as a PDE constrained optimization for a family of deformations. The PDE constraint is deduced from the discretization of the covariant derivative of the velocity in the tangential direction along a geodesic. Finite elements are used for the spatial discretization, and a hierarchical minimization strategy together with a Lagrangian multiplier type gradient descent scheme is implemented. The method is applied to the analysis of root growth in botany and the morphological changes of brain structures due to aging.

Building on concepts from continuum mechanics, we offer a computational model for geodesics in the space of thin shells, with a metric that reflects viscous dissipation required to physically deform a thin shell. Different from previous work, we incorporate bending contributions into our deformation energy on top of membrane distortion terms in order to obtain a physically sound notion of distance between shells, which does not require additional smoothing. Our bending energy formulation depends on the so-called relative Weingarten map, for which we provide a discrete analogue based on principles of discrete differential geometry. Our computational results emphasize the strong impact of physical parameters on the evolution of a shell shape along a geodesic path.

The concept of a shape space is linked both to concepts from geometry and from physics. On the one hand, a path-based viscous flow approach leads to Riemannian distances between shapes, where shapes are boundaries of objects that mainly behave like fluids. On the other hand, a state-based elasticity approach induces a (by construction) non-Riemannian dissimilarity measure between shapes, which is given by the stored elastic energy of deformations matching the corresponding objects. The two approaches are both based on variational principles. They are analyzed with regard to different applications, and a detailed comparison is given.

In this paper concepts from continuum mechanics are used to define geodesic paths in the space of shapes, where shapes are implicitly described as boundary contours of objects. The proposed shape metric is derived from a continuum mechanical notion of viscous dissipation. A geodesic path is defined as the family of shapes such that the total amount of viscous dissipation caused by an optimal material transport along the path is minimized. The approach can easily be generalized to shapes given as segment contours of multi-labeled images and to geodesic paths between partially occluded objects. The proposed computational framework for finding such a minimizer is based on the time discretization of a geodesic path as a sequence of pairwise matching problems, which is strictly invariant with respect to rigid body motions and ensures a 1-1 correspondence along the induced flow in shape space. When decreasing the time step size, the proposed model leads to the minimization of the actual geodesic length, where the Hessian of the pairwise matching energy reflects the chosen Riemannian metric on the underlying shape space. If the constraint of pairwise shape correspondence is replaced by the volume of the shape mismatch as a penalty functional, one obtains for decreasing time step size an optical flow term controlling the transport of the shape by the underlying motion field. The method is implemented via a level set representation of shapes, and a finite element approximation is employed as spatial discretization both for the pairwise matching deformations and for the level set representations. The numerical relaxation of the energy is performed via an efficient multi-scale procedure in space and time. Various examples for 2D and 3D shapes underline the effectiveness and robustness of the proposed approach.

A variational approach to defining geodesics in the space of implicitly described shapes is introduced in this paper. The proposed framework is based on the time discretization of a geodesic path as a sequence of pairwise matching problems, which is strictly invariant with respect to rigid body motions and ensures a 1-1 property of the induced flow in shape space. For decreasing time step size, the proposed model leads to the minimization of the actual geodesic length, where the Hessian of the pairwise matching energy reflects the chosen Riemannian metric on the shape space. Considering shapes as boundary contours, the proposed shape metric is identical to a physical dissipation in a viscous fluid model of optimal transportation. If the pairwise shape correspondence is replaced by the volume of the shape mismatch as a penalty functional, for decreasing time step size one obtains an additional optical flow term controlling the transport of the shape by the underlying motion field. The implementation of the proposed approach is based on a level set representation of shapes, which allows topological transitions along the geodesic path. For the spatial discretization a finite element approximation is employed both for the pairwise deformations and for the level set representation. The numerical relaxation of the energy is performed via an efficient multi-scale procedure in space and time. Examples for 2D and 3D shapes underline the effectiveness and robustness of the proposed approach.

We introduce the covariance of a number of given shapes if they are interpreted as boundary contours of elastic objects. Based on the notion of nonlinear elastic deformations from one shape to another, a suitable linearization of geometric shape variations is introduced. Once such a linearization is available, a principal component analysis can be investigated. This requires the definition of a covariance metric - an inner product on linearized shape variations. The resulting covariance operator robustly captures strongly nonlinear geometric variations in a physically meaningful way and allows to extract the dominant modes of shape variation. The underlying elasticity concept represents an alternative to Riemannian shape statistics. In this paper we compare a standard L²-type covariance metric with a metric based on the Hessian of the nonlinear elastic energy. Furthermore, we explore the dependence of the principal component analysis on the type of the underlying nonlinear elasticity. For the built-in pairwise elastic registration, a relaxed model formulation is employed which allows for a non-exact matching. Shape contours are approximated by single well phase fields, which enables an extension of the method to a covariance analysis of image morphologies. The model is implemented with multilinear finite elements embedded in a multi-scale approach. The characteristics of the approach are demonstrated on a number of illustrative and real world examples in 2D and 3D.

Concepts from elasticity are applied to analyze modes of variation on shapes in two and three dimensions. This approach represents a physically motivated alternative to shape statistics on a Riemannian shape space, and it robustly treats strong nonlinear geometric variations of the input shapes.
To compute a shape average, all input shapes are elastically deformed into the same configuration. That configuration which minimizes the total elastic deformation energy is defined as the average shape. Each of the deformations from one of the shapes onto the shape average induces a boundary stress. Small amplitude stimulation of these stresses leads to displacements which reflect the impact of every single input shape on the average. To extract the dominant modes of variation, a PCA is performed on this set of displacements.
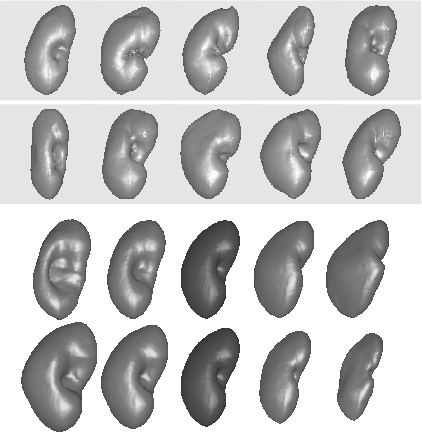
To make the approach computationally tractable, a relaxed formulation is proposed, and sharp contours are approximated via phase fields. For the spatial discretization of the resulting model, piecewise multilinear finite elements are applied. Applications in 2D and in 3D demonstrate the qualitative properties of the presented approach.

A physically motivated approach is presented to compute a shape average of a given number of shapes. An elastic deformation is assigned to each shape. The shape average is then described as the common image under all elastic deformations of the given shapes, which minimizes the total elastic energy stored in these deformations. The underlying nonlinear elastic energy measures the local change of length, area, and volume. It is invariant under rigid body motions, and isometries are local minimizers. The model is relaxed involving a further energy which measures how well the elastic deformation image of a particular shape matches the average shape, and a suitable shape prior can be considered for the shape average. Shapes are represented via their edge sets, which also allows for an application to averaging image morphologies described via ensembles of edge sets. To make the approach computationally tractable, sharp edges are approximated via phase fields, and a corresponding variational phase field model is derived. Finite elements are applied for the spatial discretization, and a multi-scale alternating minimization approach allows the efficient computation of shape averages in 2D and 3D. Various applications, e. g. averaging the shape of feet or human organs, underline the qualitative properties of the presented approach.