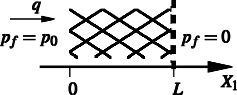
We consider steady Darcy flow of fluid through a section of poroelastic material under an applied pressure difference. In porous media flow, the superficial fluid velocity and applied pressure gradient are related by a permeability such that when the porous material is rigid, specifiying either the flow rate or the applied pressure difference allows determination of the other quantity and flow will occur for all non-zero applied pressure gradients. When the underlying solid matrix is a deformable elastic material and the fluid permeability can vary with applied strain on the solid matrix, then the permeablity can reduce to zero and the solid matrix become impermeable, so that flow is not possible and no steady solution exists. We examine existing steady poroelastic equations for a number of different well known elastic models and permeability-strain relations and consider solutions for the resulting steady strain and fluid flow. We solve the governing equations numerically for some example situations and propose a sufficient condition on the functional form of the permeability-strain relation for solutions to exist for any specified applied pressure.

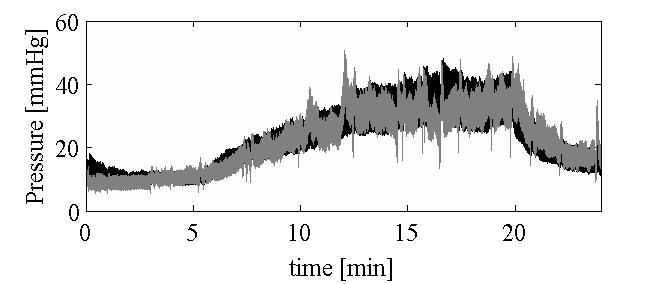In an infusion test the apparent rate of cerebrospinal fluid (CSF) production is temporarily increased through injection of fluid directly into the CSF system with the result that CSF pressure rises, in theory to a new plateau average, and the change in pressure level gives a measure of resistance to CSF outflow and the rate of approach to the plateau gives information about cerebral compliance. In the first part of this paper we give details of a two-fluid (blood and CSF) spherically symmetric poroelastic model that can simulate an infusion test which includes oscillations in blood pressure. This model has been applied to clinical data where the infusion rate and arerial blood pressure are input and an oscillatory CSF pressure is computed along with spatial parenchyma displacement, strain and local changes in CSF content. In the later part of this paper, the poroelastic model is simplified by spatial integration resulting in a one-compartment model that includes blood pressure oscillations but which, when they are ignored, reduces to a well-known one-compartment model. When the arterial pressure pulsations are included, their interaction with a non-linear compliance results in solutions that have to be interpreted very carefully to predict parameter values.

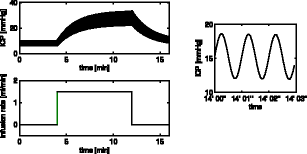
We have developed a multi-fluid model for flow of cerebrospinal fluid (CSF) in the brain which incorporates both CSF and blood pressure variations and has general application for study of hydrocephalus, and particularly here, for simulation of a CSF infusion test. Existing poro-elastic models for CSF flow treat the parenchyma and CSF as a continuum where very slow fluid flow interacts with and can affect the deformation of the underlying elastic substructure. A spherical model with CSF production at the centre of the brain, which allows flow through the aqueduct and very slow flow through the parenchyma before absorption at the outer periphery of the brain, has provided plausible results for hydrocephalus. However, while that model provides new predictions about the interior state of the parenchyma, it is only applicable for long time scales the neglect blood pulsations on the cardiac cycle time scale. Here we describe a model which, by adding a blood compartment to the usual poro-elastic framework, allows blood pulsations to be included and so to attempt a time accurate simulation of CSF pressure fluctuations during an infusion test.

This work analytically finds the spatial distribution of cerebrospinal fluid (CSF) pressure and brain displacement, as well as their evolution in time during an infusion test. The response of CSF pressure and parenchymal displacement to blood pressure pulsations is also included in the solution. We use a spherically symmetric, three-component poroelastic model of the brain, differentiating between the nerve cells as the solid matrix, the CSF, and the arterial blood. The governing equations are linearised with quasi-constant poroelastic parameters. The solution does reproduce the average intracranial pressure increase during the test as well as the rise in CSF pressure pulsation amplitudes due to transmission of blood pressure oscillations. In addition, the CSF flux into and out of the parenchyma is shown over tim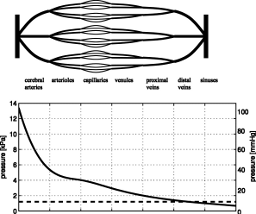e.

This work provides an analytical confirmation of the commonly used inverse power relationship between cerebral compliance and intracranial pressure. The underlying model of the compliance is based on a mechanism, in which cerebral blood vessels form the compliant part of the brain and CSF volume changes are accommodated by blood displacement into or out of the cranium. It is not intended to produce a highly accurate prediction of the intracranial pressure-volume curve, but rather to justify the phenomenological inverse power law and to give a basic interpretation of cerebral elasticity, reference pressure, and exponent of the constitutive law.

We formulate in general terms the equations for axisymmetric and fully 3D models of a hydrocephalic brain. The model is developed using small strain poroelasticity that includes non-linear permeability. The axisymmetric model is solved for four ventricle shapes, an ellipsoid, a `peanut' shape, a `cross' shape and a `bone' shape. The distribution of fluid pressure, velocity and content in the deformed parenchyma for a blocked aqueduct provides new qualitative insight into hydrocephalus. Some observations are offered for two forms of CSF abnormality, normal pressure hydrocephalus and idiopathic intracranial hypertension. The model is extended to include a gravitational term in the governing equations and the effect of hydrostatic pressure variation is considered. Results of a fully 3D simulation are described for two horn-like lateral ventricles and one case with two lateral ventricles and a third ventricle.

We examine a spherically symmetric model of the brain and apply non-linear permeability in a small strain poroelastic framework. Numerical solutions to the model show that non-linear effects tend to improve predictions of ventricle wall displacement and pressure increase in acute hydrocephalus in comparison with a constant permeability model. Our model is used to study different mechanisms for hydrocephalus: complete blockage of the aqueduct and normal pressure hydrocephalus (NPH), as well as offering observations on mechanical effects in idiopathic intracranial hypertension. In each situation it is possible to apply different parameter conditions to quantify mechanical effects that correspond to some observed symptoms. The results support and quantify ideas from Levine (2000, Ventricle size in pseudo-tumor cerebri and the theory of impaired CSF absorption. J. Neurol. Sci., 177, 85-94) on a poroelastic mechanism for some features of NPH and idiopathic intracranial hypertension.