The aesthetics of Geometric Analysis

Interview with Dr. Mario Schulz, postdoc at Mathematics Münster
Mario Schulz with 3D-printed surface models.
Mario Schulz with his 3D-printed surface models.
© MM/vl

Dr. Mario Schulz is a postdoctoral researcher in the field of Geometric Analysis. One of his passions is visualising his research topics to make them more vivid for other mathematicians and for the general public. He posts a large number of gif animations on his website, focusing on minimal surfaces with free boundaries in the unit ball.

He has 3D-printed a collection of surface models at the virtual reality lab at WWU Münster – mathematics that you can touch! He thanks the Computer Vision and Machine Learning Systems Group for their support.

Simulation of a pair of free boundary minimal surfaces with the same topology and symmetry group.
Simulation of a pair of free boundary minimal surfaces with the same topology and symmetry group.
© Mario Schulz

Where did you do your studies? How are you enjoying Münster?
I graduated from ETH Zürich in 2019 and worked as a postdoc at Queen Mary University of London before I came to Münster last September.

I already feel very much at home here in Münster and our Cluster at WWU offers an ideal research environment.

When did you "fall in love" with geometry and why?
The first time I caught a glimpse of differential geometry was several years before I even started to study math when I attended a summer school for high school students organised by "Deutsche JuniorAkademien".

Since then I have been fascinated by geometric questions.

© Mario Schulz

Could you please explain in laymen terms what one of your 3D models represents?
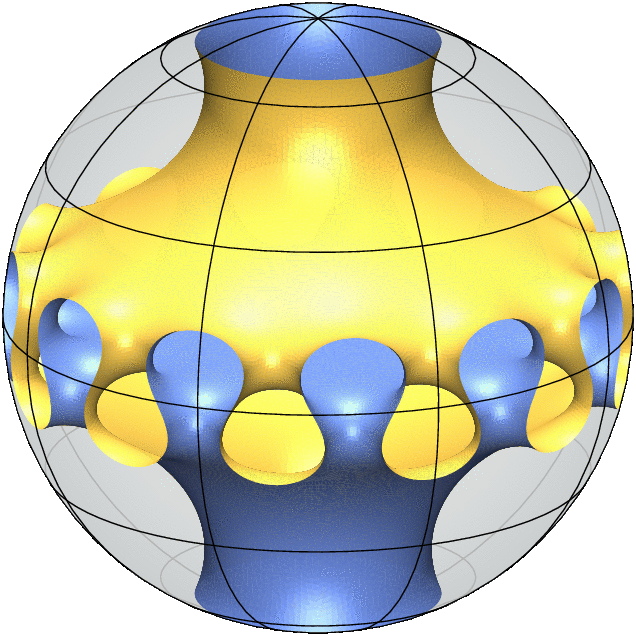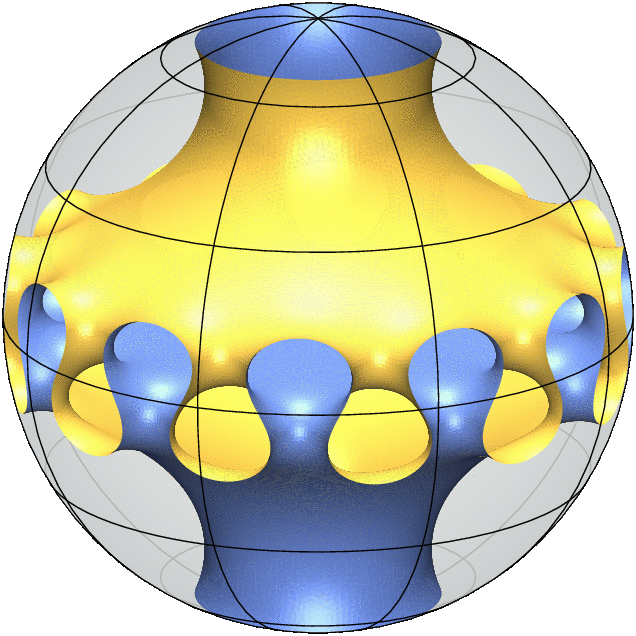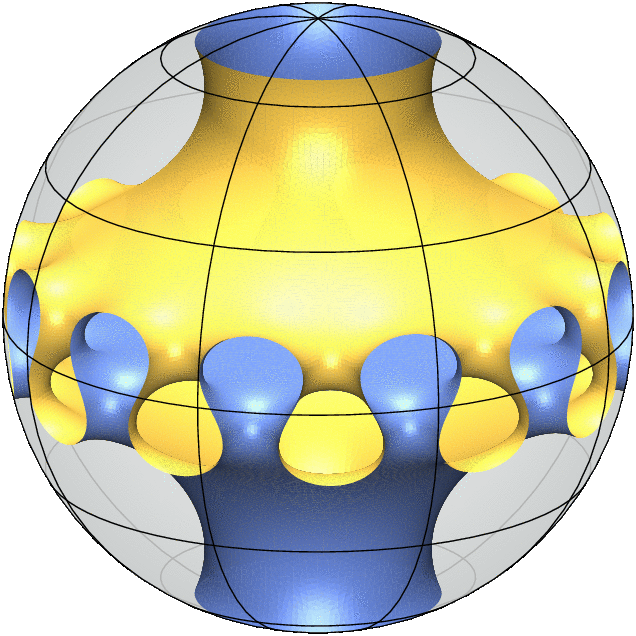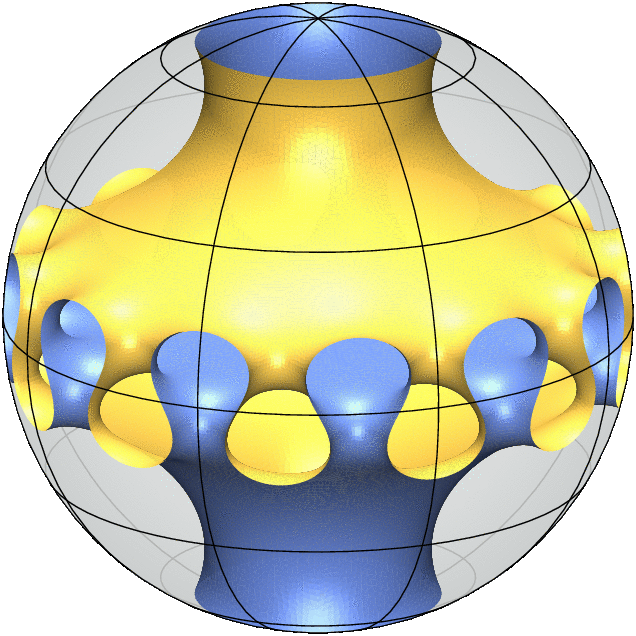
Each 3D Model is a simulation of a "free boundary minimal surface". It behaves like a soap film inside the ball and meets the sphere orthogonally along its boundary. This means that any small deformation of the surface will not decrease its area to first order.

Equivalently, the mean curvature of the surface vanishes everywhere which means that at every point on the surface there is a tangential direction in which the surface has the largest positive curvature and a second tangential direction, orthogonal to the first, in which the surface has an equal amount of negative curvature. As a consequence of this equality, minimal surfaces are particularly aesthetic and enjoy rich geometric and analytic properties.

Mario Schulz uses his 3D Models to explain the ideas in the proof to his colleagues from other mathematical fields.
Mario Schulz uses his 3D Models to explain the ideas in the proof to his colleagues from other mathematical fields.
© MM/vl

Do you have a "dream theorem " - one that you dream of proving in the future?
The existence and uniqueness question interests me the most. Does the unit ball contain embedded free boundary minimal surface with any given topology (i.e. the number of boundary components and number of holes) and are such embeddings unique up to ambient isometry if they exist?

My most recent joint work with Alessandro Carlotto and David Wiygul from ETH Zürich answers the general uniqueness questions in the strongest negative terms by providing infinitely many pairs of non-isometric free boundary minimal surfaces with the same topology and symmetry group. (The gif animations above illustrate this result.)

Yet for the simplest examples of free boundary minimal surfaces one could still hope for uniqueness up to congruence and in fact it would be a dream result to fully prove the uniqueness of the "critical catenoid", a free boundary minimal annulus in the unit ball.

Links:
The private webpage of Dr. Mario Schulz with lots of visualisations of topics in geometric analysis

Differential Geometry Group at the University of Münster

Computer Vision and Machine Learning Systems Group at the University of Münster