Mathematics and medical imaging

"Mathematics for a better world" – that is this year’s motto for International Mathematics Day. A good example of this is medical progress, where mathematics makes important contributions – for example in medical imaging, the topic which is at the heart of the next online talk in the series "Brücken in der Mathematik" given by the Cluster of Excellence Mathematics Münster.
On March 24, Prof. Dr. Benedikt Wirth, Professor of Mathematical Optimization, will then be presenting (in German) the fundamental mathematical findings which were necessary for the development of technologies. In the following interview he gives a small advance insight into these mathematical concepts and describes the specific research projects in which he is carrying out research with colleagues from the fields of biology, medicine and other disciplines.
Benedikt Wirth, without revealing too much of your talk, what were the mathematical concepts and ideas which gave medical imaging a decisive push forward?
When medical imaging technologies such as computer tomography (CT), magnetic resonance imaging (MRI) or ultrasound are used, a sort of computation is made of what the body looks like from the inside. There are many comparable situations in which a sought magnitude cannot be measured but has to be calculated from indirect measuring – typically by solving one or more equations. Some of these problems are very old, for example calculating the radius of the Earth. Even in the case of such simple problems, it’s helpful to have a basic understanding of when equations can, or cannot, be solved. It’s also helpful to have an understanding of statistics in order to be able to handle the inevitable measuring errors. In the case of medical or related imaging, there is an additional special feature: the sought magnitude represents not only a number, or perhaps a handful of numbers – but rather, an entire image has to be reconstructed. This is where the concept of – and an understanding of – so-called compact operators is helpful: the measuring process in medical imaging can be described as one of these. I’ll be saying more about these concepts in my talk.
What other mathematical progress is there in this field?
Medical imaging would be inconceivable without efficient algorithms. This comprises discoveries and developments ranging from the fast Fourier transform to more recent methods of so-called convex optimization. The idea of non-smooth regularization – in other words, a kind of improvement of the image reconstruction without blurring the contours – has also brought significant progress and went hand in hand with new mathematical concepts. At the moment we can see how deep learning and data-driven methods are having more and more success in supporting image reconstruction. Here too we expect decisive progress to be made.
What are the current problems that you’re working on in the field of medical imaging?
Within the Collaborative Research Centre "inSight", what we’re looking at in particular is generating images of objects which move or are subject to temporal change. This is becoming increasingly important in medical imaging: on the one hand, we’re more and more interested in observing changes over time such as the changing distribution of immune cells, and on the other it’s becoming increasingly important today – with the spatial and temporal resolutions now possible when measuring – to recognise and compensate for even small or rapid movements in the object being measured. Nowadays, images of static objects can, in most cases, be reconstructed very satisfactorily – bit there’s still work to be done on problems involving time-dependency.
And what exactly does your research involve?
What we’re looking at specifically – in two collaborative projects with physicians, biologists and physicists – are, on one side, conventional medical positron emission tomography and, on the other, microscopy of living tissue. The long-term vision in the first project is to be able to trace individual, radioactively marked cells in a patient’s body, for example leucocytes or metastatic cells in tumours. From a mathematical view, this requires methods of image reconstruction to be developed for which, at any given time, only a few measurements can be taken, but which – if we incorporate all the timepoints available – nevertheless enable good spatial and temporal resolution. For this purpose, we use methods of so-called optimal transport and try to prove quantitative and qualitative statements on the reconstruction.
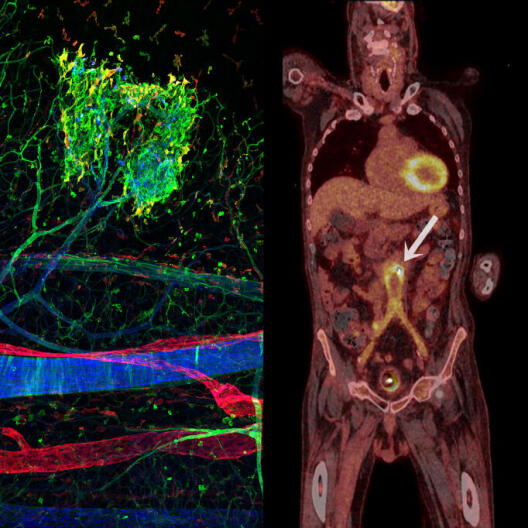
The vision in the second project is to be able to carry out microscopy on a pulsating blood vessel or even on twitching muscles – despite the movements involved – and, as a result, gain an understanding of cellular processes in atherosclerosis, for example. What is needed here, from a mathematical point of view, are mathematical models with the ability to efficiently describe, predict and ultimately correct a motion. To this end we use classical concepts such as interpolation between the datapoints measured, combined with more recent, geometrically motivated, views of the set of all the movements which can occur.
In the TraCAR project, researchers from mathematics, biology and medicine are working together on immunotherapies to treat cancer. What contribution can mathematics make here?
The project is investigating immunotherapies for solid tumours, i.e. abnormal masses of tissue – in contrast to leukaemia, where immunotherapy is already very successful. The idea is for the body’s own, genetically modified immune cells to combat the tumour. In principle, mathematics can help on three levels here:
Firstly: in imaging, new mathematical methods of reconstruction improve the spatial and temporal resolution. This is first of all necessary for evaluating the biomedical experiments. In later phases, it may be helpful in diagnostics or in monitoring the progress of the therapy. What we want to know is what happens to the immune cells, where they end up, and whether they are active.
Secondly: the mathematical modelling and examination of the models created can deliver insights into what scenarios can occur in principle during immune cell therapy and what happens in these scenarios. These models are of course based on data previously collected and on biomedical findings. In doing so, we’re looking for answers to fundamental questions such as whether the tumour can in principle be completely eradicated, or whether even – in another scenario – an opposite effect might take place.
Thirdly: Based on the mathematical models, therapies can be optimized by means of mathematical optimization and numerical simulation. For every patient, for example, we would like to optimize the quantity and the type of immune cells, or the time – or times – when the therapy is carried out.
At the moment we‘re still at the beginning, at the first stage. Here, too, we are developing and examining methods of reconstructing the temporal movement of immune cells. In contrast to the project I mentioned before in the Collaborative Research Centre, what we are trying out here are other, more geometrical, approaches.
One challenge in interdisciplinary projects is no doubt the different specialist terms and concepts. What happens in practice? Is there first a meeting at the start of the project to find a common "language"?
Interdisciplinary projects don’t start overnight. They’re based on years of interaction in which the participants get to know both one another and the problem or problems involved. First of all, you simply have discussions with people from disciplines which are closely related or more remote, for example on a personal level at your own university. This doesn’t necessarily happen with the aim of embarking on a project together, but rather out of interest: you’re just taking a look at things outside your own particular field. Sometimes interesting, longer discussions arise, which can even turn into mutual one-to-one tuition; occasionally, interdisciplinary seminars or workshops are organized specifically, at which the specialists give easy-to-understand presentations to representatives of all the disciplines involved. In the course of time, you learn a little bit of the other language – enough, at any rate, to be able to make yourself understood in an interdisciplinary project. If the project takes on a concrete form, you read a bit of the project partners’ specialist literature in order to understand the problem in its entirety.
Incidentally, in a common project the disciplines don’t interact all the time. As a rule, very little interaction is needed when the mathematician spends a few months trying to prove features of the reconstruction method, or when the biomedical specialist tries to produce new immune cells and establish an experimental protocol. Interaction tends to become more important when relevant interim results have been achieved in the individual disciplines, and you look and see whether these results are useful for the overall project or still need to be improved on.
Links:
Livestream "Blick in den Körper: Über das Inverse und medizinische Bildgebung" 24 March 2021, 7:30 pm, Livestream
CRC inSight: Multiscale imaging of organ-specific inflammation

