Complex Geometries

 When solving of PDEs on time dependent domains or domains with a complex shape, classic Finite Element Methods pose many problems regarding the construction of the mesh. During the last decade a range of different methods have been developed to decouple the construction of a finite element mesh, i.e. the finite element discretization, from the geometrical details of the domain.

One approach, our group is working on, is the Unfitted Discontinuous Galerkin method. It offers the possibility to compute simulations with a fine structures on a relatively coarse mesh and was used for the solution of elliptic, parabolic and hyperbolic problems. Using the UDG approach it is easily possible to run simulations directly on image data, e.g. micro-CT images, or to combine it with level-set or phase-field methods to handle moving interfaces.

Multi-Physics Problems

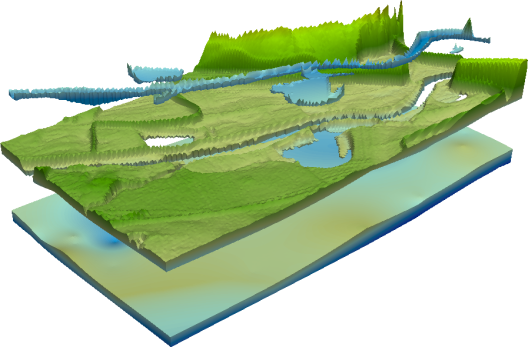
In the course of multi-physics applications the efficient coupling of different PDEs on different sub-domains is getting more important. We are working on different aspects of domain decomposition methods and their implementation, either for parallelization and preconditioning, or for the coupling in a multi-physics setting. The latter also includes heterogenous coupling of sub-domains of different dimension.

Efficient PDE Software

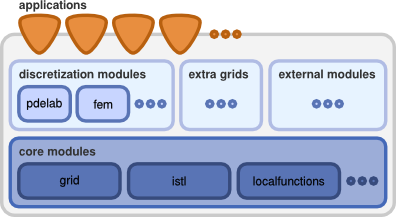
We set high value on the development of efficient FEM software. Reusability and interoperability of and with existing software are very important. In this course we are actively participating in the development of the C++ FEM framework DUNE.

Programming with C++ and using generic programming techniques, allows us to use fine grained interfaces and still employ optimization techniques, like inlining and loop-unrolling. This is the basis for sustainable and efficient software development.

High Performance Computing

The speed of a single processor stopped growing in the last years, instead modern chips include many cores to increase the performance. At the same time the architecture of high performance computers like the BlueGene is changing, they include acceleration processors which leaves us with a heterogeneous hardware system. Modern scientific software must cope with these changing requirements. As it is too much a burden to expect scientist to rewrite their code for each new hardware, the software design and the numerical algorithms must be adopted in a way that allows us to port our software with as small work as possible, while still retaining a reasonable performance boost.