MiRA+: Professionelle Kompetenz zum Lehren mathematischen Modellierens
Den Ausgangspunkt des hier vorgestellten Evaluationskonzepts bilden neu implementierte Lehr-Labore zum mathematischen Modellieren. In ihnen wird in einer länderübergreifenden Kooperation (gemeinsam mit der Universität Koblenz-Landau, Klock & Siller, 2016) der Frage nachgegangen, inwieweit sich Aspekte professioneller Kompetenz angehender Lehrkräfte zum mathematischen Modellieren durch reflektierte Praxis fördern lassen.
Theoretisches Konstrukt
Einige spezifische Fähigkeiten und Fertigkeiten, die angehende Lehrer*innen zum Unterrichten mathematischen Modellierens erwerben sollen, fassen Borromeo Ferri und Blum (2009) in einem vierdimensionalen Kompetenzmodell zusammen.
Nach diesem Modell benötigen Lehrkräfte in einer theoretischen, einer aufgabenbezogenen, einer unterrichtsbezogenen und einer diagnostischen Dimension unterschiedliche Teilkompetenzen zum Lehren mathematischer Modellierung.
Die Untersuchung von Aspekten professioneller Kompetenz angehender Lehrkräfte – im Sinne dieses Modells – legt ein Konstrukt nahe, welches sich an einem etablierten Modell zur Messung professioneller Kompetenz von Mathematiklehrkräften orientiert, wie z.B. von Baumert und Kunter (2011) entwickelt. Durch die Synthese beider Modelle wurde das in Abbildung 1 dargestellte Konstrukt definiert, welches die professionelle Kompetenz zum Lehren mathematischer Modellierung empirisch messbar macht.
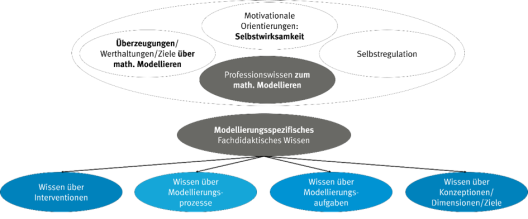
Die einzelnen Aspekte des obigen Konstrukts werden in einem quasi-experimentellen Prä-Post-Kontrollgruppen-Design mithilfe eines quantitativen Paper-Pencil-Fragebogens erhoben. Die Seminarinhalte sind aufeinander abgestimmt, sodass beide Versuchsgruppen ein vergleichbares Treatment erfahren.
Konzeptionell unterteilt sich das Lehr-Labor MiRA+ (Mathematik in realen Anwendungen) in eine Vorbereitungs-, eine Praxis- und eine Nachbereitungsphase (s. Abbildung 2). Den Mittelpunkt aller Phasen bilden Modellierungsprozesse auf der einen sowie die Sensibilisierung für und der Umgang mit Heterogenität in ihren verschiedenen Dimensionen auf der anderen Seite.
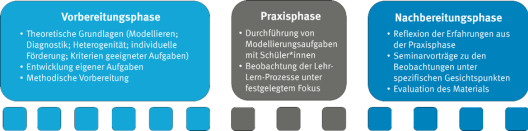
Die eingesetzten Modellierungsaufgaben eignen sich dabei insbesondere für einen produktiven Umgang mit Heterogenität innerhalb von Lerngruppen, indem sie eine nach Vorkenntnissen, Interessen und Leistungsfähigkeit differenzierte bzw. individualisierte Lernumgebung schaffen.
Literatur
Baumert, J. & Kunter, M. (2011). Das Kompetenzmodell von COACTIV. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Hrsg.), Professionelle Kompetenz von Lehrkräften – Ergebnisse des Forschungsprogramms COACTIV (S. 29-54). Münster: Waxmann.
Borromeo Ferri, R. & Blum, W. (2009). Mathematical modelling in teacher education - experiences from a modelling seminar. In Proceedings of CERME 6 (S. 2046-2055). Lyon, France.
Klock, H. & Siller, H. (2016). Lehr-Lern-Labore für eine praxisnahe forschungsbezogene Lehrer*innen-Ausbildung. MoSAiK-Teilprojekt der Universität Koblenz-Landau im Rahmen der gemeinsamen “Qualitätsoffensive Lehrerbildung” von Bund und Ländern. [http://mosaik.uni-koblenz-landau.de]

