 |
Combining 2D synchrosqueezed wave packet transform with optimization for crystal image analysisWe develop a variational optimization method for crystal analysis in atomic resolution images, which uses information from a 2D synchrosqueezed transform (SST) as input. The synchrosqueezed transform is applied to extract initial information from atomic crystal images: crystal defects, rotations and the gradient of elastic deformation. The deformation gradient estimate is then improved outside the identified defect region via a variational approach, to obtain more robust results agreeing better with the physical constraints. The variational model is optimized by a nonlinear projected conjugate gradient method. Both examples of images from computer simulations and imaging experiments are analyzed, with results demonstrating the effectiveness of the proposed method.
|
 |
A convex, lower semi-continuous approximation of Euler's elastica energyWe propose a convex, lower semi-continuous, coercive approximation of Euler's elastica energy for images, which is thus very well-suited as a regularizer in image processing. The approximation is not quite the convex relaxation, and we discuss its close relation to the exact convex relaxation as well as the difficulties associated with computing the latter. Interestingly, the convex relaxation of the elastica energy reduces to constantly zero if the total variation part of the elastica energy is neglected.
Our convex approximation arises via functional lifting of the image gradient into a Radon measure on the four-dimensional space Ω×S1×R, Ω⊂R2, of which the first two coordinates represent the image domain and the last two the normal and curvature of the image level lines. It can be expressed as a linear program which also admits a predual representation. Combined with a tailored discretization of measures via linear combinations of short line measures, the proposed functional becomes an efficient regularizer for image processing tasks, whose feasibility and effectiveness is verified in a series of exemplary applications. |
 |
Redistancing dynamics for vector-valued multilabel segmentation with costly fidelity: grain identification in polycrystal imagesA novel numerical method for multilabel segmentation of vector-valued images is presented. The algorithm seeks minimizers for a generalization of the piecewise-constant Mumford--Shah energy and is particularly appropriate for energies with a fitting (or fidelity) term that is computationally expensive to evaluate. The framework for the algorithm is the standard alternating-minimization scheme in which the update of the partition is alternated with the update of the vector-valued constants associated with each part of the segmentation. The update of the partition is based on the distance function-based diffusion-generated motion algorithms for mean curvature flow. The update of the vector-valued constants is based on an Augmented Lagrangian method. The scheme automatically chooses the appropriate number of segments in the partition. It is initialized with a partition of many more segments than are expected to be necessary. Adjacent segmentations of the partition are merged when energetically advantageous. The utility of the algorithm is demonstrated in the context of atomic-resolution polycrystalline image segmentation.
|
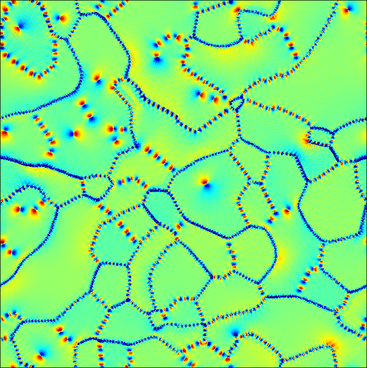 |
Fast automated detection of crystal distortion and crystal defects in polycrystal imagesGiven an image of an atomic crystal, we propose a variational method which at each image location determines the local crystal state and which localizes and characterizes crystal defects. In particular, the local crystal orientation and elastic distortion are detected, as well as dislocations, and grain and twin boundaries. To this end an energy functional is devised whose minimization yields a tensor field G describing the local crystal strain at each point. The desired information about the local crystal state can then be read off from this tensor field; in particular, its curl provides information about grain boundaries and dislocations. As is typical for variational image processing, the energy functional is composed of a fidelity and a regularization term. It has a simple L2-L1 type structure so that its minimization can be performed via a split Bregman iteration. GPU parallelization results in short computing times.
|
 |
Segmentation of Crystal Defects via Local Analysis of Crystal DistortionWe propose a variational method to simultaneously detect dislocations and grain boundaries in an image of a crystal as well as the local crystal distortion. To this end we extract a distortion field F from the image which is nearly curl-free except at dislocations and grain boundaries. The sparsity of the curl is promoted by an L1-regularization of curl(F) in the employed energy functional. The structure of the functional admits a fast and parallelizable minimization such that fairly large images can be analyzed in a few minutes.
|
 |
Convex relaxation of a class of vertex penalizing functionalsWe investigate a class of variational problems that incorporate in some sense curvature information of the level lines. The functionals we consider incorporate metrics defined on the orientations of pairs of line segments that meet in the vertices of the level lines. We discuss two particular instances: One instance that minimizes the total number of vertices of the level lines and another instance that minimizes the total sum of the absolute exterior angles between the line segments. In case of smooth level lines, the latter corresponds to the total absolute curvature. We show that these problems can be solved approximately by means of a tractable convex relaxation in higher dimensions. In our numerical experiments we present preliminary results for image segmentation, image denoising and image inpainting.
|
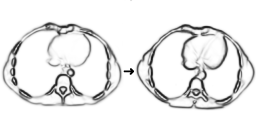 |
On the Gamma-convergence of joint segmentation and registration problemsA classical task in image processing is the following: Given two images, identify the structures inside (for instance detect all image edges or all homogeneous regions; this is called segmentation) and find a deformation which maps the structures in one image onto the corresponding ones in the other image (called registration). In medical imaging, for instance, one might segment the organs in two patient images and then identify corresponding organs in both images for automated comparison purposes. The image segmentation is classically performed variationally using the Mumford-Shah model, and the obtained structures are then mapped onto each other by minimizing a registration energy in which the deformation is regularized via elasticity. Experimentally it often seems more robust to perform segmentation and registration simultaneously so that both can benefit from each other. The question to be examined here is: Can phase field approximations of the Mumford--Shah model be used for the joint segmentation and registration problem? The answer is yes and no; we mathematically analyse corresponding generic phase field models and reveal interesting phenomena that might impair the quality of the results for some of the models. These phenomena are characteristic of coupling phase fields with deformations and thus are interesting in their own right.
In more detail, there are essentially two phase field approximations for the Mumford-Shah model: The Modica-Mortola approximation, in which the phase field encodes the homogeneous image regions, and the Ambrosio-Tortorelli approximation, in which the phase field encodes the image edges. If one combines the phase field segmentation functionals with an image registration term, in which the matching deformation is regularized via a hyperelastic energy, then the following can be observed: As the phase field parameter ε tends to zero, the joint segmentation and registration functional based on Modica-Mortola phase fields Γ-converges exactly against the expected sharp interface limit and thus represents a feasible model. Using Ambrosio-Tortorelli phase fields, however, we see three distinct effects, the first two already in 1D: (1) The phase field profile is sqeezed by the matching deformation so that part of the phase field will be ignored. (2) Spurious ghost phase fields occur which in the Γ-limit reduce the weighting parameter of the matching term. (3) In 2D, a string of phase field dots can be dilated tangentially to a full phase field edge, ultimately resulting in the lack of any registration in the Γ-limit. |

