 |
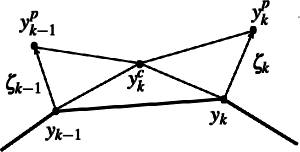
Differentiable piecewise-Bezier surfaces on Riemannian manifoldsWe generalise the notion of Bezier surfaces and surface splines to Riemannian manifolds. To this end we put forward and compare three possible alternative definitions of Bezier surfaces. We furthermore investigate how to achieve C0- and C1-continuity of Bezier surface splines. Different from Euclidean space and from one-dimensional Bezier splines on manifolds, C1-continuity cannot be ensured by simple conditions on the Bezier control points, but requires an adaptation of the Bezier spline evaluation scheme. Finally, we propose an algorithm to optimise the Bezier control points if a set of points to be interpolated by a Bezier surface spline is given. We show computational examples on the sphere, the special orthogonal group, and two Riemannian shape spaces.
|
 |
Variational time discretization of geodesic calculusWe analyze a variational time discretisation of geodesic calculus on finite- and certain classes of infinite-dimensional Riemannian manifolds. We investigate the fundamental properties of discrete geodesics, the associated discrete logarithm, discrete exponential maps, and discrete parallel transport, and we prove convergence to their continuous counterparts. The presented analysis is based on the direct method in the calculus of variation, on Γ-convergence, and on weighted finite element error estimation. The convergence results of the discrete geodesic calculus are experimentally confirmed for a basic model on a two-dimensional Riemannian manifold. This provides a theoretical basis for the application to shape spaces in computer vision, for which we present one specific example.
|
 |
Discrete geodesic calculus in the space of viscous fluidic objectsBased on a local approximation of the Riemannian distance on a manifold by a computationally cheap dissimilarity measure, a time discrete geodesic calculus is developed, and applications to shape space are explored. The dissimilarity measure is derived from a deformation energy whose Hessian reproduces the underlying Riemannian metric, and it is used to define length and energy of discrete paths in shape space. The notion of discrete geodesics defined as energy minimizing paths gives rise to a discrete logarithmic map, a variational definition of a discrete exponential map, and a time discrete parallel transport. This new concept is developed in the context of shape spaces with shapes that are described via deformations of a given reference shape, and it is applied to a particular shape space in which shapes are considered as boundary contours of physical objects consisting of viscous material. The flexibility and computational efficiency of the approach is demonstrated for topology preserving shape morphing, the representation of paths in shape space via local shape variations as path generators, shape extrapolation via discrete geodesic flow, and the transfer of geometric features.
|
 |
Optimization methods on Riemannian manifolds and their application to shape spaceWe extend the scope of analysis for linesearch optimization algorithms on (possibly infinite-dimensional) Riemannian manifolds to the convergence analysis of the BFGS quasi-Newton scheme and the Fletcher--Reeves conjugate gradient iteration. Numerical implementations for exemplary problems in shape spaces show the practical applicability of these methods.
|

