Pioneering work: mathematical fundamentals of light refraction

Something everyone learns in Physics lessons at school is that light is refracted and reflected at the interface between air and water. The reason for this is the different refractive indices which the two mediums have – an optical property which is characteristic of each material. There are also materials with so-called negative refraction indices. These are special optical properties which the materials have which can make objects invisible and inaudible. “The mathematical understanding of this topic is still in its infancy,” says Dr. Barbara Verfürth from the Institute of Analysis and Numerics at the University of Münster. Her PhD thesis demonstrates pioneering mathematical work by making her the first person to calculate the connection between materials and their refraction. This fundamental work in the field of mathematics can help later in developing high-resolution microscopes – or in improving sound-absorbing walls, which are important for good acoustics in concert halls or recording studios.

From simulation to application

Back in 1968, the Russian physicist Victor Veselago already described the existence of materials with so-called negative refractive indices, thus opening up an entirely new field of research into metamaterials. These are artificially produced materials whose permeability for electrical and magnetic fields deviates from that which occurs in materials present in nature. What is needed to understand and calculate the unusual wave propagation in materials with negative refraction indices is, on the one hand, very complex materials consisting of at least two individual materials with nanofine internal structures, and, on the other hand, so-called numerical multiscale methods. These are special methods developed for problems in which there occur processes over both large and small areas and are linked to one another. By using this method, the nanofine structures of the materials can be appropriately determined.

Before Barbara Verfürth, together with her colleagues, simulated these materials on the computer with varying ray and wave optics, she had previously been working for weeks on equations and numerical methods with the aim of understanding a certain mathematical problem – in this case, negative refraction. “Right from the beginning I was fascinated by the physical phenomenon of negative refraction, and I wanted to have a better understanding of how it occurs,” says the 27-year-old mathematician. “That’s why I simulated this scientific process on the computer, enabling me to formulate mathematically precise statements on the quality of these simulations.” The simulations confirm the accuracy of her calculations and, as a result, make the applicability of the method clear. On the basis of this simulation it can be seen that the unusual properties of the material are due to special resonance effects. “This means that at some parts of the material the wave is stronger than in the rest of the material. This in turn leads to the energy of the wave being heavily concentrated on certain sub-areas,” Verfürth explains.

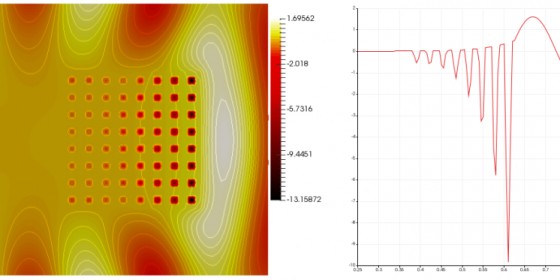
Her work provides fundamental help to other mathematicians because her tried-and-tested method can be used for future research in the field of wave propagation in complex materials. In particular, the structure of the underlying equations and their solutions help physicists and other users to have a better understanding of phenomena observed in experiments and, even before any experiment, to predict results on the basis of computer simulations.

Further information

• Original publication: Verfürth B. 2018. “Numerical multiscale methods for Maxwell's equations in heterogeneous media”; dissertation, University of Münster.
• Workgroup for Numerical Analysis & Scientific Computing (Prof. Mario Ohlberger)