One term – three different interpretations

As different as the term “dynamic” is used and understood in science, so diverse are the research areas of the University of Münster, in which dynamic even plays a central role in the title. Prof. Christopher Deninger and Prof. Mario Ohlberger from the Cluster of Excellence „Mathematics Münster“, the lawyer Prof. Nils Jansen from the Cluster of Excellence „Religion and Politics“ and the biochemist Prof. Lydia Sorokin from Cells-in-Motion Cluster of Excellence explain what they understand by the term in their research.

 

Cell Dynamics in Homeostasis, Inflammation and Infection

We investigate dynamics in the behaviour of cells in organisms. Cells are constantly on the move and adapt to new situations: They divide and move within an organism. They interconnect with other cells and develop into different tissues and organs. In order for tissues and organs to function correctly, cells must act collectively in highly complex processes. We investigate how genes and molecules determine a cell’s properties and behaviour and how the dynamic cellular processes in an organism remain in healthy balance, which is called homeostasis. We also analyse how healthy cellular systems can develop into diseased systems. Here, we are especially interested in inflammation, during which immune cells migrate out of blood vessels into tissues to fight infections or to repair tissue damage. However, inflammatory reactions vary, depending on the organ and the vessel type in which they occur. To be able to watch cells at work we use and develop imaging methods. Central to our field of research is the development of new chemical and mathematical methods that can be employed in different imaging methods and, thus, also have the potential to be transferred from application in fruit flies, zebrafish and mice to clinical imaging methods for exploitation in patient diagnosis.

Additionally, there is another dynamic dimension in our research: The cooperation of scientists from very different disciplines brings an incredible amount of motion into our scientific field. In the past years, we have broken down the traditional boundaries between disciplines and now experience how questions and results from different disciplines drive and advance each other: Biomedical researchers identify molecules critical for specific cellular processes, chemists develop new substances that bind to such molecules or cells to make them visible, and mathematicians and computer scientists develop algorithms which use artificial intelligence to analyse the resulting large quantities of complex imaging data. In this way, a computer may recognize specific patterns of cell behaviour in many different tissues that are not otherwise visible and, thereby, we can identify new biomedical questions and research directions.

Author: Prof. Lydia Sorokin

 

Mathematics Münster. Dynamics – Geometry – Structures

Within mathematics, dynamics -- or more precisely dynamical systems -- are understood as spaces together with transformations that map the points of the space to other positions. If the transformations can be reverted, the dynamics are called reversible and the transformations are called symmetries. Examples of symmetries are rotations or reflections of geometric objects, but also the symmetries of algebraic equations that are still not fully understood. In general, symmetries serve as a fundamental organizing principle. A well-known example is the symmetry group of Rubik’s cube. The group is rather large with more than 43.000.000.000.000.000.000 symmetries, but its structure is completely understood. In mathematical terms the group is:

 

 

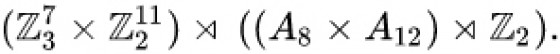
Based on this description it is  possible for example to prove that at most 20 moves are sufficient to solve the cube, i.e. to return any position to the one with faces of equal colour. Of course the symmetries, that we are analysing in the cluster of excellence are more complicated and much less understood.

In many cases, the transformations describing the dynamics are not reversible. This means that information gets lost under their application. In such cases, we are particularly interested in the long time behaviour of the dynamical system: If the transformation is applied over and over again, the system develops with each action of the transformation. This development can be seen as a temporal evolution of the system in discrete time steps. Analogously, continuous dynamical systems occur which can be viewed as continuous temporal evolutions. In this way it is possible for example to formalize the time evolution of the universe in a mathematical model. All “parabolic” partial differential equations give rise to continuous dynamical systems. These parabolic equations arise in a host of problems from the natural sciences within applied mathematics. They are equally important in theoretical mathematics, for example in the study of the Ricci flow, which has led to spectacular breakthroughs in our understanding of three dimensional spaces. An important research direction in the cluster Mathematics Muenster: Dynamics – Geometry – Structure concerns the generalization of Ricci flow techniques to higher dimensional spaces, and their applications.

Author: Prof. Christopher Deninger/Prof. Mario Ohlberger

 

Religion and Politics. Dynamics of Tradition and Innovation

In the new Cluster phase, we examine the historically changing relationship between religion and politics. The central questions we are looking at are: In which way can religion stimulate, curb and modify social and political conflicts? Where lies its dynamic power? Which external conditions facilitate or restrict its capacity to mobilize people?

Using this approach, we want to focus our attention on the active role of religion in political and social conflicts in societies. Thus, we pursue an approach which significantly differs from other theoretical approaches, such as secularization theories, which tend to treat religion as a traditional entity which merely reacts to social changes. In contrast to such an understanding, we ask how religion – possibly also under conditions of increasing disbelief and decreasing affiliation to religious denominations – is able to facilitate or inhibit social and political change, and how religion changes under changing circumstances. When we talk about the dynamics of religion, therefore, we mean its power to accelerate or reinforce social processes and conflicts or, conversely, soften such processes and facilitate reconciliation.

This means that, at the same time, the focus turns towards the dynamic interaction between religious tradition and innovation. Traditions can themselves become a source of innovation; innovations can be hidden under a screen of traditions, yet innovations have to legitimize themselves in the context of tradition. Paying special attention to the inherent dynamics of the religious includes paying attention to political, social and economic contexts as well. The dynamics of religious change can only be explained on the basis of the interaction between religious and extra-religious factors.

Last but not least, our studies aim at identifying specific forms of religious change. We reconstruct the interdependence and differentiation of religion and non-religious social spheres; we analyse modes of conflict and reconciliation – but also modes of intermixture, transformation, criticism and self-criticism. And, finally, we ask how the dynamics of religion can be politically and legally regulated in diverse cultural contexts.

Author: Prof. Nils Jansen