g. What is Bose Einstein Condensation?

 

Now we come to the really interesting part. I think it already became obvious that the chemical potential and the distribution functions, especially the Bose-Einstein distribution function play an essential role in Bose-Einstein condensation.

Let us consider what happens to the occupation number N_i at the point ε_i=μ with different statistics. For this treatment it is helpfull to use the mathematical limit concept.

Fermi-Dirac:

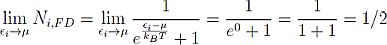
In Fermi Dirac statistics the chemical potential marks the energy level where the probability to find a particle drops to 50%. In this context the chemical potential is often called Fermi Energy.

Now comes the interesting part, what happens to the Bose Einstein statistics at this point:

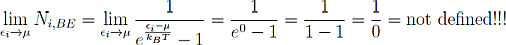
It is obvious that Bose-Einstein statistics fail at this point. Albert Einstein the inventor of Bose-Einstein statistics pointed this out in the same paper where he published the formula for N_i,BE called “Quantentheorie des einatomigen idealen Gases erste und zweite Abhandlung” [de] (“Quantum theory of the ideal one-atomic gas first and second part.”) in 1924. For his calculations he used a physical and mathematical concept developed by Satyendra Nath Bose. That's where the name Bose Einstein Statistics and -Condensation comes from.

At the same time he proposed a solution for this problem. For good physical reasons, which are not so easy to explain, he claimed that in such a system all particles that do not fit inside this distribution before it gets undefined will collect in the lowest energy state. This means that in our gas an essential part of the particles will have exactly the same energy, and when I say exactly I really mean exactly.  This additional particles in the lowest energy state form the Bose Einstein Condensate.

In this sense the chemical potential marks the energy at which Bose Einstein Condensation occurs. The chemical Potential is not a constant, so it is also possible to change it in such a way that it reaches the lowest energy state in order to get a Bose Einstein Condenstion.

But Einstein didn’t consider other consequences which became obvious when Bose-Einstein condensation was first realized by Anderson et.al. in 1995. At this point it is worth mentioning that Helium also undergoes a phase transition similar to a Bose Einstein Kondensation at temperatur slightly above the absolute zero point.

We already pointed out one important aspect, that’s the occupation of the lowest energy state with a huge number of particles which can even nearly reach the number of particles in the considered gas. This means that under some conditions nearly all particles in our system occupy the lowest energy state.

This is also the main signature for BEC. Before BEC the lowest energy state is only occupied by a small fraction of particles in the gas. When BEC occurs this fraction becomes huge and can reach nearly 100% although it can never reach truly 100% except at zero Kelvin.

Another very important property is coherence and correlation of the particles in the condensate. Coherence means that the waves of the individual particles in the condensate interfere constructively with each other. Correlation means that each particle in the condensate “feels” what the others do and is strongly influenced by them.

This two properties result in a so called “macroscopic wave function”. This means that all the particles in the condensate can be described by one wave function instead of describing each particle by an individual wave function. And as a BEC can contain millions of particles it is possible to observe quantum effects on a large scale, while normally one is restricted to look at single atoms or electrons in order to observe quantum effects.

Now we know, at least theoretically, what a Bose Einstein Condensation is. The next question we have to ask is:

How can one achieve the conditions for Bose Einstein Condensation?