f. What are the distribution functions in many body systems?
An important question in statistical mechanics is how the energy of the whole many particle system distributes over the individual particles? Or in other words what are the energies of the individual particles?
To answer this question distribution functions were developed. As already mentioned in the section about bosons and fermions the nature of the particles is essential. Consequently the distribution functions vary between systems of bosons, fermions and classical particles.
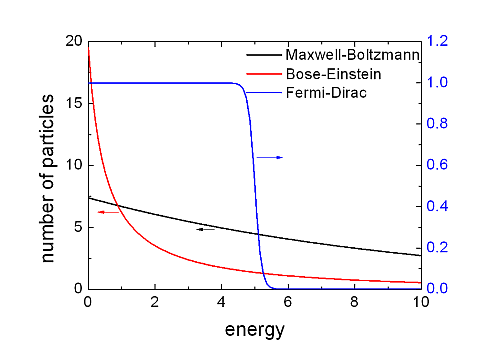
A good example for a classical particle system is an atomic gas (for example oxygen atoms) under standard conditions. Its energy distribution can be described by the Maxwell-Boltzmann distribution.
A well known system of fermionic particles is the, nearly free, electron gas in a conductor at room temperature which is best described by the Fermi-Dirac distribution, while we can treat a photon gas in a black body as an ideal bosonic system which obeys Bose-Einstein statistics.
In the figure the three distribution functions are presented. Let’s point out the peculiarities of these distribution functions by using some maths.
The Maxwell Boltzmann distribution is described by the following equation:
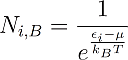
With this formula one can calculate how many particles N_i can be found in the considered system with energy εi in thermal equilibrium with the chemical potential μ and the temperature T.
I already pointed out several times that these theories are statistical. Of course it is not possible to find a half or quarter of a particle in an energy state. Instead one should interpret these values rather as probabilities. If Ni becomes 1 it means that we can find one particle with energy ei for sure. If its zero, we will find no such particle with this energy for sure. For values between one and zero there is just a certain probability to find a particle in that energy state. For Ni=0,4 for example there is a chance of 40% to find a particle with this energy. For values of Ni that are greater than one, we will find several particles with this energy. Another important point is that the energy is noted in a moving coordinate system, so energy zero means average energy.
In a similar manner one can write down the distribution functions for Fermions:
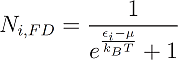
And for Bosons:
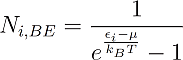
The indices B, FD and BE stand for Boltzmann, Fermi-Dirac and Bose-Einstein.
One can see that the only distinction between them is just the addend +1 or -1 in the denominator, but this changes everything. One can see for example that in Fermi-Dirac statistics Ni,FD lays always between 1 and zero. This is obvious, because the denominator can never become smaller than one, since
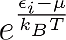
is always positive. This means that in a many particle system composed of Fermions two particles can never have the same energy, unless they differ in another quantum number but it would be too much to point this out here and it’s not necessary for our discussion.
From the figure it seems that the difference between Bose-Einstein statistics and Maxwell-Boltzmann statistics is just a quantitative and not a qualitative one, but this is not completely true, as I will point out in the next section which deals with the question:

