c. What is quantum statistics?
Classical statistical mechanics describe a lot of phenomena connected with many body systems. Its predictions are very accurate as long as the mean distance between atoms is much greater than the so called deBroglie wavelength.
This quantity reflects directly the quantum nature of matter, especially the concept of wave particle duality. The deBroglie wavelength connects classical particle physics and quantum mechanical wave physics, as it associates each particle with a wavelength
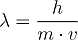
where l denotes the deBroglie wavelength, m the mass and v the velocity of a particle. The letter h stands for the Planck constant invented by Max Planck in 1900.
We already learned that we can easily determine the mean velocity of a particle in a gas by simply measuring the temperature of the gas.
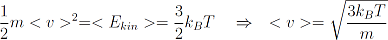
With this relation we can determine the deBroglie wavelength of a particle (atom or molecule) with mass m in a gas with temperature T.
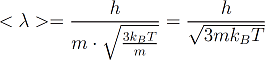
This quantity is also call "thermal deBroglie wavelength" as it is caused by thermal movement. Let’s calculate the thermal deBroglie wavelength of let’s say oxygen at 20°C that’s 293.15K.
The mass of an oxygen atom can be looked up in any periodic table of elements. If we now take the value of 16 g/mol from the periodic table we still don’t know the mass of each individual oxygen atom, to calculate this we first have to know what a mol is.
A mol is simply a definite quantity of atoms namely 6·1023 (again a 6 with 23 zeros behind it). This means that 6·1023 oxygen atoms together have a mass of 16g. To calculate the mass of one oxygen atom we have to divide these two numbers and get 2.7∙10-23g for one oxygen atom and as oxygen atoms bond together and form oxygen molecules the mass of the molecules is twice that big.
With this numbers we get λ=8.2∙10-13 m=0.00000000082mm which is even smaller than the radius of the molecule. This means that in our everyday world quantum statistics doesn’t play any role. It is nearly impossible to compress a gas so much, that the distance between neighbouring atoms becomes smaller than their radius. But it happens in neutron stars and black holes, but we don’t want to consider those cases here.
So the above discussion seems to be only of academic nature and has nothing to do with the real world right? WRONG!
We have already seen that the thermal deBroglie wavelength is not a constant, but depends on certain parameters. We cannot change the Boltzmann or the Planck constant, as they are fundamental physical constants. Till now there is no possibility to change the mass of an atom, unless we replace it with another atom or isotope. But we can change the temperature of a gas.
We know from classical statistical mechanics, that the mean distance between particles in a gas under standard-conditions is of the order of 10∙10-9 m=10nm. In order to observe quantum mechanical effects in such a gas we have to reduce the temperature drastically. We can even calculate this temperature by demanding that the thermal deBroglie wavelength has to become equal to the mean particle distance.
In our case:
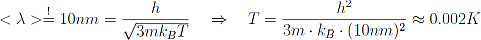
Just to point this out: Zero K is the lowest possible temperature, since it corresponds to a mean particle velocity of zero, and one cannot be slower than that.
This means at a temperature of 2mK the classical theory fails and we have to use a quantum mechanical theory.
One could still interject that this theory has nothing to do with everyday life, since it is only needed under extreme conditions. But atoms are not the only particles that can form a gas.
It is known that electrons in a conductor can also be treated as an electron-gas. The peculiarity of this system is that electrons are 2000times lighter and their density is about 100times larger than that of atoms in a gas. This leads to a critical temperature where quantum effects start to play an important role of about 10,000°C. This means that if we want to describe a metal at room temperature (~20°C) we have to use quantum statistics in order to describe the system accurately.
This is one of the reasons why microelectronics and especially devices as solid state transistors started to develop shortly after quantum mechanics where invented. Quantum mechanics was a necessary tool to understand electrical phenomena on the microscopic level what finally led to microelectronics.
In quantum statistics particles are divided into two cathegories. Thus the next section deals wit the question:

