b. What is statistical mechanics?
What do phases and phase transitions have in common with statistics one might ask. In everyday life we associate statistics with something unnatural invented by bureaucrats to put things and people into categories. But this is not correct; in fact statistics are something very natural and are helpful to explain a lot physical phenomena which are connected with many particle systems. In this sense phases and phase transitions arise from statistics.
If for example one wants to describe the expansion of a gas or a liquid which contains about 1019 particles per cubic centimeter (that’s a one with nineteen zeros) one does not have the slightest chance to describe every particle separately. But one can make very good statistical statements about the system.
For example the temperature of an ideal gas in thermal equilibrium is defined as the mean kinetic energy of the particles in the gas divided by a constant called Boltzmann constant so-named after one of the founders of statistical mechanics Ludwig Boltzmann.
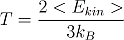
The bracket around the energy variable indicates that it’s the mean energy of all particles in the system. So it turns out that it is nearly impossible to measure the kinetic energy of each particle individually, but it is very easy to measure the mean kinetic energy.
We can extend this concept to various other parameters like density and pressure. One can even drive this further and describe more complex physical properties like magnetism, superconductivity etc. and the related phase transitions.
In conclusion statistical mechanics is a basis to understand physics in many particle systems. As phases are in this sense properties only present in ensembles of many particles we need statistics to understand them and to determine theoretically what conditions are necessary to undergo a phase transition.
Statistical Mechanics as it is presented here, is a classical theory. This means that quantum effects are not included. As quantum effects are neccessary for Bose Einstein Condensation, the next section will deal with the question:

