Die laut Revisionsplan turnusmäßige Evaluation wurde erfolgreich durchgeführt und die Phase der Datenerhebung und -auswertung mit einer intensiven Beratung durch einen Qualitätszirkel abgeschlossen. Geprüft wurde, inwieweit Überarbeitungen des Modells oder gar eine völlige Neukonzeption notwendig sind. Auch die Koordination der Modellentwicklung und etablierte Kommunikationsstrukturen standen auf dem Prüfstand.

Die Zusammenfassung des Abschlussberichts dieser umfassenden Evaluation können Sie nun an dieser Stelle herunterladen. Weiterführende Dokumente finden sich im Aufklapper "Aktuelle Evaluation".
Evaluation des Zeitfenster-Modells für das Praxissemester - Zusammenfassung (PDF)

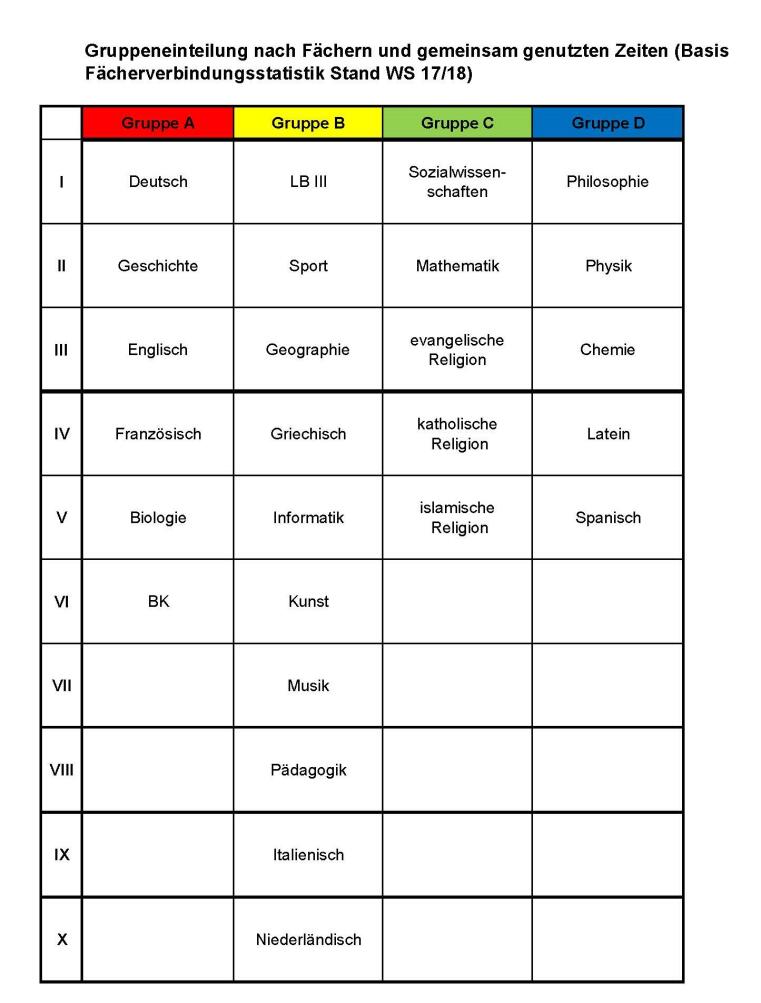
Zeitfenstermodell zum Praxissemester

Die Studierenden im Praxissemester belegen gemäß Praxissemester-Ordnung in ihren beiden studierten Fächern sowie in den Bildungswissenschaften jeweils ein Begleitseminar: die Praxisbezogenen Studien.

Bei der Vielzahl der möglichen Fächerverbindungen und des Lehrangebots für –  in Vollauslastung – rund 800 Studierende je Semester bleiben zeitliche Überschneidungen zwischen den Praxisbezogenen Studien nicht aus. Dies bringt Studierende in eine schwierige Situation, da der Besuch der Begleitveranstaltungen verpflichtend ist. Auch für die Fächer bedeutet es im Vorfeld einen hohen Planungsaufwand, wenn sie mit den zahlreichen möglichen Kombinationsfächern bilaterale Absprachen treffen müssten. Dies würde zu einem hohen Verwaltungsaufwand und zu Zeitverzögerungen im gesamten Planungsprozess führen.  

Daher soll ein Zeitfenstermodell ein möglichst überschneidungsfreies Lehrveranstaltungangebot systematisch, effektiv und mit geringem Aufwand gewährleisten. Die Planung der Lehrveranstaltungen im Praxissemester erfolgt bereits seit Oktober 2015 auf der Basis eines Zeitfenstermodells.

• Grundlagen der Modellierung

  Ziel ist es, eine möglichst geringe Überschneidung von Lehrveranstaltungen zum Praxissemester zu erreichen. Dafür ist es notwendig, folgende grundlegende Planungsparameter zu berücksichtigen:  

  • Studierendenstatistik nach gewählten Fächerverbindungen (Auswertung auf der Basis der Studierendenzahlen von vier Immatrikulationszeitpunkten)
  • Einschätzungen zum konkret benötigten Lehrveranstaltungsangebot
  • Fachspezifische Planungsparameter

  Damit werden sowohl statistische Daten als auch die Selbsteinschätzungen der Fächer berücksichtigt, sodass das Modell gleichermaßen die Anforderungen an eine grundsätzliche Standardisierung über die Fächer hinweg und an eine fachbezogene Individualisierung erfüllt.
  
  Auf der Basis dieser Informationen wurden den Fächern bzw. Fächergruppen (vgl. Aufklapper "Die durchgangsbezogene Anwendung des Modells") bestimmte Zeiten zugewiesen, deren Einhaltung zu einem für die Studierenden zeitlich disjunkten Lehrangebot führt. Fächer mit einem anzahlmäßig großen Umfang des Lehrangebots erhalten dabei Zeiten zur flexiblen Nutzung; Fächer mit einem einfachen Lehrangebot erhalten besonders geschützte, d.h. zu ausschließlich durch diese Fächer zu nutzenden Zeiten.

  Das Modell wächst mit:
  Zur weiteren Optimierung des Zeitfenstermodells wird der Kommunikationsprozess zwischen dem ZfL und den Fächern der Lehramtsstudiengänge regelhaft zu ausgewiesenen Zeitpunkten so fortgeführt, dass Anpassungen für die künftige Planung vorgenommen werden können. Hinsichtlich des Modellteils für die Studientage weitet sich die Kommunikation und Abstimmung auf die Bezirksregierung mit Blick auf die Zentren für schulpraktische Lehrerausbildung (ZfsL) aus.
  
  Außerdem erfolgt immer dann eine Modifikation des Modells, wenn auf veränderte äußere Rahmenbedingungen, wie z.B. eine Erweiterung der zulässigen Fächerverbindung oder des Studienangebots durch neue Studienfächer, reagiert werden muss.

  Ein Revisionsplan systematisiert die unterschiedlichen Anlässe, Fristen und Instrumente für die Qualitätssicherung und damit Optimierung des Modells.

   

   

• Vorteile des Modells

  Durch Prüfung der Studierendenstatistik in den einzelnen Fächerverbindungen der vergangenen Erstimmatrikulationen konnte das Überschneidungsrisiko bestimmt werden. Ein hohes Risiko besteht dann, wenn in häufig studierten Fächerverbindungen ein hoher Anteil der Studierenden von etwaigen terminlichen Überschneidungen betroffen sind. Durch eine datenbasierte Einteilung der Fächer in Gruppen (vgl. Aufklapper Das Modell und Benutzungshinweise) mit möglichst geringen Überschneidungsrisiko konnte eine Überschneidungsminimierung von im Durchschnitt 96% (fachspezifische Unterschiede von mindestens 91% bis zu 100%) erzielt werden.

• Die durchgangsbezogene Anwendung des Modells

  Um nicht jedem Fach eine eigene Zeit zuweisen zu müssen, werden die Fächer, die nicht miteinander studiert werden können oder faktisch nicht kombiniert werden, in Gruppen eingeteilt. Die Fächer jeder Gruppe teilen sich somit die zugewiesenen Zeiten. Mögliche verbliebene Überschneidungen zwischen Fächern innerhalb einer Gruppe, die sich aufgrund der zahlreichen zulässigen Fächerverbindungen dennoch ergeben könnten, werden durch besondere Zeiten („Geschützte Zeiten“) verhindert, die insbesondere den Fächern mit einfachem Lehrangebot zugeteilt werden.

   

  

  Das Zeitfenstermodell 2.0, das seit Einführung der Praxissemester-Ordnung 2018 besteht, ist grundsätzlich auf Dauer, d.h. zeit- und terminunabhängig angelegt, um den Aufwand für semesterweise Anpassungen oder Aktualisierungen möglichst gering halten zu können. Dies gilt in gleicher Weise für das Modell 2.1 ab Februar 2025.

  Dennoch ist eine semester- und durchgangsabhängige Anwendung des Modell notwendig, die die einzelnen Praxissemesterwochen sowie konkrete Termindaten ausweist. Darin sind auch ausführliche Erläuterungen und Planungshilfen enthalten. So kann planungssicher mit dem Modell gearbeitet werden.

  Zeitfenstermodell/ Anwendung Praxissemester-Durchgang Februar 2025

  Zeitfenstermodell Praxissemester-Durchgang September 2024

  Zeitfenstermodell Praxissemester-Durchgang Februar 2024

  Zeitfenstermodell Praxissemester-Durchgang September 2023

  Zeitfenstermodell Praxissemester-Durchgang Februar 2023

   

   

   

   

   

   

   

   

   

   

   

   

   

• Support

  Sie …
  … haben Fragen bzgl. der Anwendung des Modells?
  … benötigen Unterstützung bei der Nutzung der angebotenen Zeiten?
  … suchen nach individuellen Lösungen?
  
  Wir …
  … unterstützen beim Finden zusätzlicher Lösungen.
  … geben Anleitung zur Nutzung des Modells.
  … beraten bei kurzfristigen Terminverschiebungen.
   

  Individuell und lösungsorientiert

  Das Zeitfenstermodell entlastet Sie davon, nach geeigneten Terminen für Ihre Veranstaltungen im Praxissemester, die Praxisbezogenen Studien zu suchen, in denen die Studierenden keine Überschneidungen mit den Praxisbezogenen Studien ihrer anderen beiden Fächer erleben. Nicht immer aber gelingt dies hundertprozentig und nicht immer entsprechen die zugewiesenen Zeitslots den Wünschen der Fächer. Je größer ein Fach ist und je mehr Veranstaltungen es anbietet, desto mehr Planungsaufwand besteht. Und wenn die Gruppe der Lehrenden sehr heterogen ist, sind auch umso mehr individuelle Bedarfslagen zu berücksichtigen.
  
  Dies kann ein zentrales und hochgradig schematisiertes Instrument leider nicht leisten. Zwar wird das Zeitfenstermodell regelmäßig evaluiert, optimiert und an sich verändernde äußere Rahmenbedingungen angepasst, aber dennoch ist manchmal ein persönlicher Support gefragt, der sich auf Ihre Interessen als Lehrende einstellt, ohne die vorrangigen Interessen der Studierenden aus dem Blick zu verlieren.

  Das Modell bietet viele individuelle Lösungsmöglichkeiten: Der persönliche Support durch das Zeitfensterteam im ZfL hilft Ihnen dabei.

  Wir nehmen uns für Sie Zeit!
  Kontaktieren Sie uns gerne - Sie erreichen uns unter zeitfenster.zfl@uni-muenster.de .

  Simone Mattstedt
  Abteilung Praxisphasen
  Hammer Str. 95
  48153 Münster
  Zimmer 205
  Tel.: +49 251 83-32519

• Zeitfensterkoordinator*innen nach Fächern

  Zeitfenster-Koordinator*innen sind an der Weiterentwicklung des Zeitfenstermodells zum überschneidungsfreien Studieren der Lehrveranstaltungen im Praxissemester beteiligt und setzen die Vorgaben des Zeitfenstermodells in den Lehrveranstaltungen ihres Faches um. Sie sind auch Ansprechpersonen für Studierende bei Fragen zu Überschneidungen von Lehrveranstaltungen.

  Stand: 14.01.2019

  Dr. Markus Bohlmann (Philosophie)
  Dr. Dirk Eikmeyer (Mathematik)
  Faris Mansouri (Islam. Religionslehre)
  Dr. Marion Golenia (Sport)
  Dr. Patrick Gollub (Bildungswissenschaften)
  Stephanie Guballa (Berufliche Fachrichtungen)
  Dr. Jan-Bernd Haas (Chemie)
  Dr. Georg Harbig (Musik)
  Prof. Dr. Stefan Heusler (Physik)
  Stefan Hölscher, Wiebke Lammert  (Kunst)
  Dr. Erhard Holze (Evang. Religionslehre)
  Dr. Guido Hunze (Kath. Religionslehre)
  Dr. Karl-Philipp Kamps (Deutsch)
  Prof. Dr. Corinna Koch (Romanistik)
  Prof. Dr. Frauke Matz (Englisch)
  Janina Pawelzik (Sachunterricht)
  Dr. Susanne Pinkernell-Kreidt, Dr. Bente Lucht (Griechisch/Latein)
  Dr. Marie-Louise Poschen, Sven Kohnen (Niederländisch)
  Dr. Karin Meendermann (Sozialwissenschaften)
  Prof. Dr. Jörn Schützenmeister, Dr. Judith Küper (Pädagogik)
  Dr. Maria Sieverdingbeck (Biologie)
  Prof. Dr. Marco Thomas (Informatik)
  Dr. Christian Winklhöfer (Geschichte)
  Dr. Katja Wrenger (Geographie)

Publikation

Gemeinsam mit dem HRK-Projekt nexus Übergänge gestalten, Studienerfolg verbessern und dem Netzwerk Überschneidungsfreies Studieren an Hochschulen konnte ein HRK-nexus Impulsheft gestaltet werden, was nun veröffentlicht wurde. Es steht auf der Website des HRK-Projekts nexus zum Download zur Verfügung und kann dort auch als Printausgabe bestellt werden.