Seismic wave propagation using Micropolar theory
Our group in Münster applies micropolar theory to study elastic wave propagation phenomena in presence of microstructure. Micropolar theory is a generalization of the classical linear elastic theory, where each particle has an intrinsic rotational degree of freedom, called micro-rotation and/or spin, and which depends on the so-called Cosserat couple modulus that characterizes the micropolar medium. The theory assumes that this spin field is different from the continuum rotation.
Elastic wave propagation in crystal structures is described by two types of modes: the acoustic one and the optic one. In the acoustic type (longitudinal acoustic LA and/or transverse acoustic TA), all the atoms in the unit cell move in phase, this means that the atoms move coherently in the lattice, resulting in the deformation of the lattice (see Figure 1). In the optic type (longitudinal optic LO and/or transverse optic TO), the atoms move out of phase (see Figure 1). In micropolar theory, we relate the frequency at which the optic modes are observed in laboratory experiments to the cut-off frequency.
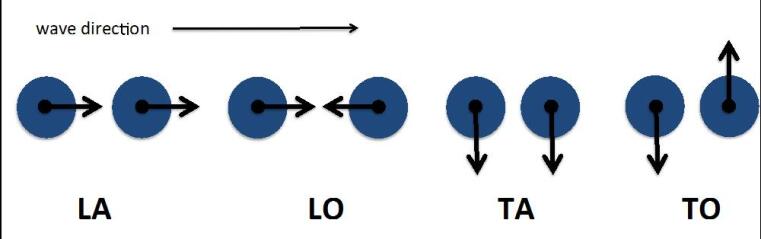
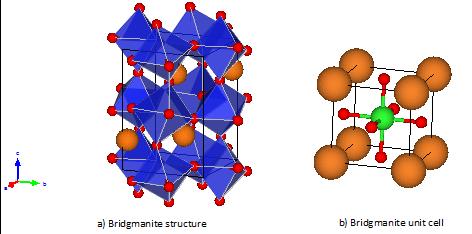
The presence of micropolar effects in crystalline solids have been observed through several laboratory experiments like X-ray diffraction, neutron diffraction, specific heat measurements and infra-red and Raman spectroscopy. In several Raman spectroscopy experiments done on bridgmanite, micropolar and microstretch behaviour of the SiO6 octahedron (see the crystal structure of bridgmanite in Fig. 2) have been observed (e.g., Karki et al. 2000).
One of the main drawbacks of using micropolar theory for the description of the elastic wave propagation is the lack of knowledge of the micropolar elastic constants and their physical interpretations. This problem has been addressed in several studies (Erinen 1999, Pouget et al. 1986) however, no general agreement is found in the literature.
In our group, we determine micropolar elastic constants for deep Earth’s mantle-like material based on experimental mineral physics results.
References
Chen, Y., Lee, J. D., & Eskandarian, A. (2004). Atomistic viewpoint of the applicability of microcontinuum theories. International journal of solids and structures, 41(8), 2085-2097.
Eringen, A. C. (1999). Microcontinuum field theories: I. Foundations and Solids. Springer Science & Business Media.
Karki, B. B., Wentzcovitch, R. M., De Gironcoli, S., & Baroni, S. (2000). Ab initio lattice dynamics of MgSiO 3 perovskite at high pressure. Physical Review B, 62(22), 14750.
Pouget, J., Aşkar, A., & Maugin, G. A. (1986). Lattice model for elastic ferroelectric crystals: continuum approximation. Physical Review B, 33(9), 6320.

