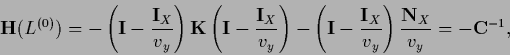Next: Kernels for
Up: Initial configurations and kernel
Previous: Truncated equations
Contents
For 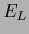 we have the truncated equation
we have the truncated equation
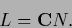 |
(688) |
Normalizing the exponential of the solution gives
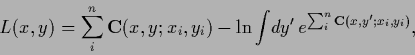 |
(689) |
or
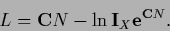 |
(690) |
Notice that normalizing 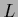 according to Eq. (689)
after each iteration
the truncated equation (688)
is equivalent to a one-step iteration with uniform
according to Eq. (689)
after each iteration
the truncated equation (688)
is equivalent to a one-step iteration with uniform  =
= 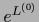 according to
according to
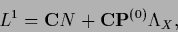 |
(691) |
where only
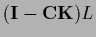 is missing from the
nontruncated equation (683),
because the additional
is missing from the
nontruncated equation (683),
because the additional  -independent term
-independent term
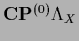 becomes inessential if
becomes inessential if 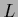 is normalized afterwards.
is normalized afterwards.
Lets us consider as example the choice
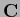 =
=
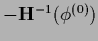 for uniform initial
for uniform initial 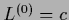 corresponding to a normalized
corresponding to a normalized  and
and
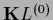 =
= 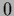 (e.g., a differential operator).
Uniform
(e.g., a differential operator).
Uniform 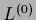 means uniform
means uniform 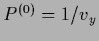 ,
assuming that
,
assuming that
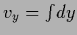 exists
and, according to Eq. (137),
exists
and, according to Eq. (137),
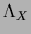 =
= 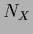 for
for
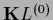 =
= 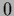 .
Thus, the Hessian (161) at
.
Thus, the Hessian (161) at 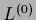 is found as
is found as
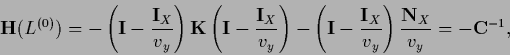 |
(692) |
which can be invertible due to the presence of the second term.
Another possibility is to start with an
approximate empirical log-density, defined as
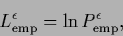 |
(693) |
with
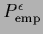 given in Eq. (239).
Analogously to Eq. (686),
the empirical log-density may for example also be smoothed
and correctly normalized again,
resulting in an initial guess,
given in Eq. (239).
Analogously to Eq. (686),
the empirical log-density may for example also be smoothed
and correctly normalized again,
resulting in an initial guess,
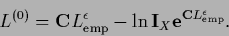 |
(694) |
Similarly, one may let a kernel 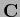 ,
or its normalized version
,
or its normalized version
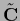 defined below in Eq. (698),
act on
defined below in Eq. (698),
act on 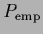 first and then take the logarithm
first and then take the logarithm
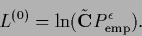 |
(695) |
Because already
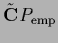 is typically
nonzero it is most times not necessary to work here
with
is typically
nonzero it is most times not necessary to work here
with
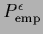 .
Like in the next section
.
Like in the next section
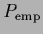 may be also be replaced by
may be also be replaced by
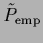 as defined in Eq. (238).
as defined in Eq. (238).




Next: Kernels for
Up: Initial configurations and kernel
Previous: Truncated equations
Contents
Joerg_Lemm
2001-01-21
![]() we have the truncated equation
we have the truncated equation
![]() =
=
![]() for uniform initial
for uniform initial ![]() corresponding to a normalized
corresponding to a normalized ![]() and
and
![]() =
= ![]() (e.g., a differential operator).
Uniform
(e.g., a differential operator).
Uniform ![]() means uniform
means uniform ![]() ,
assuming that
,
assuming that
![]() exists
and, according to Eq. (137),
exists
and, according to Eq. (137),
![]() =
= ![]() for
for
![]() =
= ![]() .
Thus, the Hessian (161) at
.
Thus, the Hessian (161) at ![]() is found as
is found as