



Next: Normalization by parameterization: Error
Up: Gaussian prior factor for
Previous: Gaussian prior factor for
Contents
Lagrange multipliers: Error functional 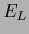
In this chapter
we look at density estimation problems
with Gaussian prior factors.
We begin with a discussion of functional priors
which are Gaussian in probabilities
or in log-probabilities,
and continue with general Gaussian prior factors.
Two sections are devoted to
the discussion of
covariances and means of Gaussian prior factors,
as their adequate choice is essential for
practical applications.
After exploring some
relations of Bayesian field theory and empirical risk minimization,
the last three sections introduce
the specific likelihood models of
regression, classification,
inverse quantum theory.
We begin with a discussion of Gaussian prior factors in 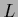 .
As Gaussian prior factors correspond
to quadratic error (or energy) terms,
consider an error functional with a quadratic regularizer in
.
As Gaussian prior factors correspond
to quadratic error (or energy) terms,
consider an error functional with a quadratic regularizer in 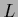
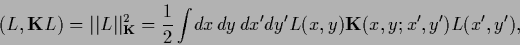 |
(106) |
writing for the sake of simplicity
from now on 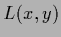 for the log-probability
for the log-probability 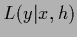 =
=
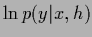 .
The operator
.
The operator 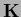 is assumed symmetric and positive
semi-definite and positive definite on some subspace.
(We will understand positive semi-definite to include symmetry
in the following.)
For positive (semi-)definite
is assumed symmetric and positive
semi-definite and positive definite on some subspace.
(We will understand positive semi-definite to include symmetry
in the following.)
For positive (semi-)definite 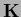 the scalar product
defines a (semi-)norm
by
the scalar product
defines a (semi-)norm
by
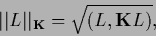 |
(107) |
and a corresponding distance by
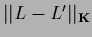 .
The quadratic error term (106)
corresponds to a Gaussian factor of the prior density
which have been called the specific prior
.
The quadratic error term (106)
corresponds to a Gaussian factor of the prior density
which have been called the specific prior
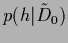 =
=
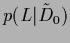 for
for 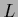 .
In particular, we will consider here the posterior density
.
In particular, we will consider here the posterior density
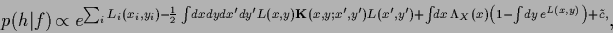 |
(108) |
where prefactors like 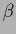 are understood to be included in
are understood to be included in 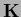 .
The constant
.
The constant 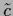 referring to the specific prior is determined
by the determinant of
referring to the specific prior is determined
by the determinant of 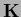 according to Eq. (70).
Notice however that not only the likelihood
according to Eq. (70).
Notice however that not only the likelihood 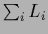 but also the complete prior
is usually not Gaussian
due to the presence of the normalization conditions.
(An exception is Gaussian regression, see Section 3.7.)
The posterior (108) corresponds to an error functional
but also the complete prior
is usually not Gaussian
due to the presence of the normalization conditions.
(An exception is Gaussian regression, see Section 3.7.)
The posterior (108) corresponds to an error functional
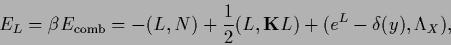 |
(109) |
with likelihood vector (or function)
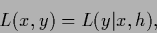 |
(110) |
data vector (function)
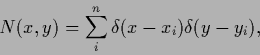 |
(111) |
Lagrange multiplier vector (function)
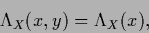 |
(112) |
probability vector (function)
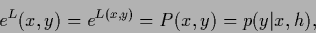 |
(113) |
and
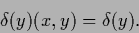 |
(114) |
According to Eq. (111) 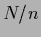 =
= 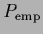 is an empirical density function
for the joint probability
is an empirical density function
for the joint probability 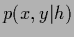 .
.
We end this subsection by defining some notations.
Functions of vectors (functions) and matrices (operators),
different from multiplication,
will be understood element-wise
like for example 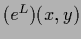 =
=  .
Only multiplication of matrices (operators)
will be interpreted as matrix product.
Element-wise multiplication has then to be written
with the help of diagonal matrices.
For that purpose we introduce diagonal matrices
made from vectors (functions)
and denoted by the corresponding bold letters.
For instance,
.
Only multiplication of matrices (operators)
will be interpreted as matrix product.
Element-wise multiplication has then to be written
with the help of diagonal matrices.
For that purpose we introduce diagonal matrices
made from vectors (functions)
and denoted by the corresponding bold letters.
For instance,
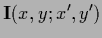 |
 |
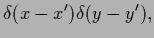 |
(115) |
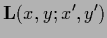 |
 |
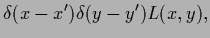 |
(116) |
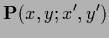 |
 |
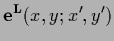 |
(117) |
| |
 |
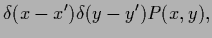 |
(118) |
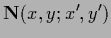 |
 |
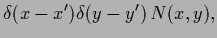 |
(119) |
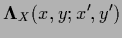 |
 |
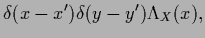 |
(120) |
or
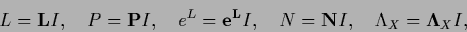 |
(121) |
where
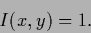 |
(122) |
Being diagonal all these matrices commute with each other.
Element-wise multiplication can now be expressed as
In general this is not equal to
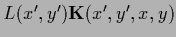 .
In contrast, the matrix product
.
In contrast, the matrix product 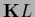 with vector
with vector 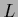
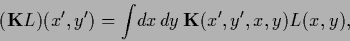 |
(124) |
does not depend on  ,
,  anymore,
while the tensor product or outer product,
anymore,
while the tensor product or outer product,
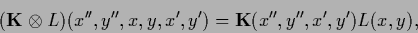 |
(125) |
depends on additional
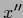 ,
,
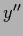 .
.
Taking the variational derivative of (108)
with respect to 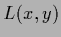 using
using
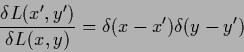 |
(126) |
and setting the gradient equal to zero
yields the stationarity equation
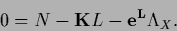 |
(127) |
Alternatively, we can write
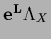 =
=
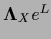 =
=
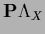 .
.
The Lagrange multiplier function 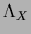 is determined
by the normalization condition
is determined
by the normalization condition
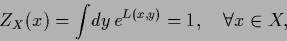 |
(128) |
which can also be written
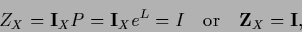 |
(129) |
in terms of normalization vector,
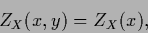 |
(130) |
normalization matrix,
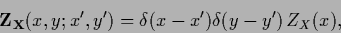 |
(131) |
and
identity on 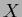 ,
,
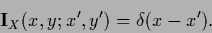 |
(132) |
Multiplication of a vector with 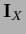 corresponds to
corresponds to  -integration.
Being a non-diagonal matrix
-integration.
Being a non-diagonal matrix
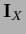 does in general not commute
with diagonal matrices like
does in general not commute
with diagonal matrices like 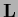 or
or 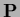 .
Note also that despite
.
Note also that despite
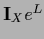 =
=
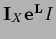 =
= 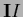 =
= 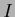 in general
in general
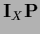 =
=
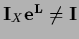 =
= 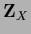 .
According to the fact that
.
According to the fact that
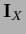 and
and
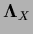 commute, i.e.,
commute, i.e.,
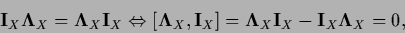 |
(133) |
(introducing the commutator ![$[A,B]$](img583.png) =
= 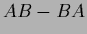 ),
and that the same holds for the diagonal matrices
),
and that the same holds for the diagonal matrices
![\begin{displaymath}[{\bf\Lambda}_X , {\bf e^L} ]=
[{\bf\Lambda}_X , {\bf P} ] = 0
,
\end{displaymath}](img585.png) |
(134) |
it follows from the normalization condition
 =
= 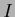 that
that
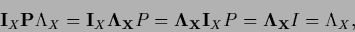 |
(135) |
i.e.,
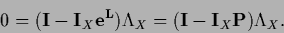 |
(136) |
For
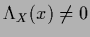 Eqs.(135,136)
are equivalent to
the normalization (128).
If there exist directions at the stationary point
Eqs.(135,136)
are equivalent to
the normalization (128).
If there exist directions at the stationary point 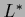 in which the normalization of
in which the normalization of 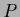 changes,
i.e., the normalization constraint is active,
a
changes,
i.e., the normalization constraint is active,
a
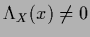 restricts the gradient
to the normalized subspace
(Kuhn-Tucker conditions
[57,19,99,193]).
This will clearly be the case for the unrestricted
variations of
restricts the gradient
to the normalized subspace
(Kuhn-Tucker conditions
[57,19,99,193]).
This will clearly be the case for the unrestricted
variations of 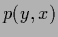 which we are considering here.
Combining
which we are considering here.
Combining
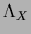 =
=
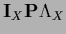 for
for
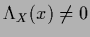 with the stationarity equation (127)
the Lagrange multiplier function is obtained
with the stationarity equation (127)
the Lagrange multiplier function is obtained
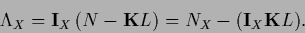 |
(137) |
Here we introduced the vector
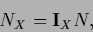 |
(138) |
with components
 |
(139) |
giving the number of data available for  .
Thus, Eq. (137) reads in components
.
Thus, Eq. (137) reads in components
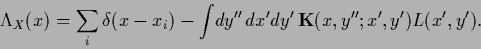 |
(140) |
We remark, that for a Laplacian 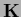 and appropriate boundary conditions
the integral term in equation (140) vanishes.
and appropriate boundary conditions
the integral term in equation (140) vanishes.
Inserting now the equation (140) for 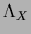 into the stationarity equation
(127) yields
into the stationarity equation
(127) yields
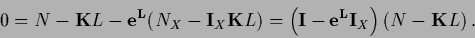 |
(141) |
Eq. (141)
possesses, besides normalized solutions we are looking for,
also possibly unnormalized solutions fulfilling 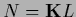 for which Eq. (137) yields
for which Eq. (137) yields 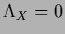 .
That happens because we used Eq. (135)
which is also fulfilled for
.
That happens because we used Eq. (135)
which is also fulfilled for
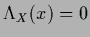 .
Such a
.
Such a
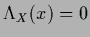 does not play the role of a Lagrange multiplier.
For parameterizations of
does not play the role of a Lagrange multiplier.
For parameterizations of  where the normalization constraint
is not necessarily active at a stationary point
where the normalization constraint
is not necessarily active at a stationary point
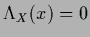 can be possible for a normalized solution
can be possible for a normalized solution 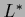 .
In that case normalization has to be checked.
.
In that case normalization has to be checked.
It is instructive to define
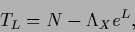 |
(142) |
so the stationarity equation (127)
acquires the form
 |
(143) |
which reads in components
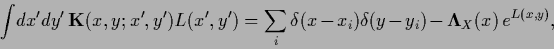 |
(144) |
which is in general a non-linear equation because 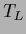 depends on
depends on 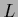 .
For existing (and not too ill-conditioned)
.
For existing (and not too ill-conditioned)
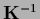 the form (143)
suggest however an iterative
solution of the stationarity equation
according to
the form (143)
suggest however an iterative
solution of the stationarity equation
according to
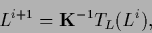 |
(145) |
for discretized 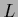 ,
starting from an initial guess
,
starting from an initial guess 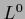 .
Here the Lagrange multiplier
.
Here the Lagrange multiplier 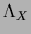 has to
be adapted so it fulfills condition (137)
at the end of iteration.
Iteration procedures will be discussed in detail
in Section 7.
has to
be adapted so it fulfills condition (137)
at the end of iteration.
Iteration procedures will be discussed in detail
in Section 7.




Next: Normalization by parameterization: Error
Up: Gaussian prior factor for
Previous: Gaussian prior factor for
Contents
Joerg_Lemm
2001-01-21
![]() .
As Gaussian prior factors correspond
to quadratic error (or energy) terms,
consider an error functional with a quadratic regularizer in
.
As Gaussian prior factors correspond
to quadratic error (or energy) terms,
consider an error functional with a quadratic regularizer in ![]()
![]() =
= ![]() .
Only multiplication of matrices (operators)
will be interpreted as matrix product.
Element-wise multiplication has then to be written
with the help of diagonal matrices.
For that purpose we introduce diagonal matrices
made from vectors (functions)
and denoted by the corresponding bold letters.
For instance,
.
Only multiplication of matrices (operators)
will be interpreted as matrix product.
Element-wise multiplication has then to be written
with the help of diagonal matrices.
For that purpose we introduce diagonal matrices
made from vectors (functions)
and denoted by the corresponding bold letters.
For instance,
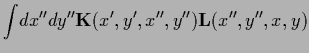
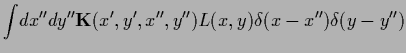
![]() using
using
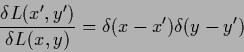
![]() is determined
by the normalization condition
is determined
by the normalization condition
![]() into the stationarity equation
(127) yields
into the stationarity equation
(127) yields