Time-resolved electron spectroscopy in Graphene with High Harmonic radiation
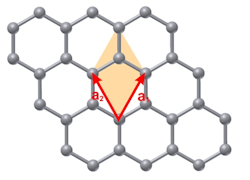
Following its experimental discovery in 2004 [1] graphene has quickly sparked interest in the scientific community. As a highly ordered two-dimensional sheet of carbon graphene offers some unique properties that make it ideally suited for various applications. These properties include a frequency-independent optical absorption of 2.3% in the visible spectrum [2], the highest known mechanical stability [3], an unusual magnetic behavior (anomalous Quantum-Hall-Effect) [4], and an extremely high electron mobility (> 200,000 cm2V-1s-1) [5]. Because of this, graphene has become one of the most promising materials for applications in electronics or optics, most notably as a very fast alternative to silicon in transistors or microchips [6].
Most of the unusual properties of graphene stem from its unique electronic band structure. The π- and π*-bands of a free standing graphene foil connect in a single point at the Fermi level (at the K-point of the Brillouin-zone). For electrons with such a momentum the dispersion is linear. Therefore, the carriers can be described as massless, relativistic particles. These so called Dirac fermions lead to the aforementioned properties.
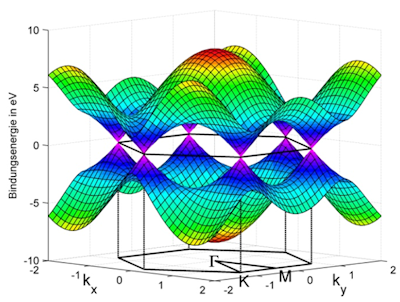
To fully understand and utilize the potential of the material one has to gain as much information about the electronic structure as possible. Because of the large attention graphene has received by the scientific community, the static electronic properties of the occupied states are well examined and understood. The dynamic properties of the unoccupied states, however, are not nearly as closely covered, not because there is no interest in them, but because the required experimental conditions are difficult to realize. In order to access the K-point in photoemission experiments one has to utilize UV radiation with photon energies of at least 11-12 eV. At the same time one needs ultrashort pulses for dynamic experiments to gain a sufficient time resolution in the order of 10-30 fs.
The experimental set-up available allows us to perform such measurements. An amplified Titanium:sapphire (Ti:Sa) laser provides the fundamental radiation (35 fs, 1.1 mJ, 6 kHz) for the generation of High Harmonics with a photon energy from 20-100 eV. The pulse duration is even shortened during the High Harmonic generation, which makes this light source ideally suited for time-resolved measurements at the edges of the Brillouin zone.
Electron dynamics are investigated with the time-resolved two-photon photoemission (TR-2PPE). With this method the pulse is separated into two parts: the pump and the probe pulse. The electrons are excited with the pump pulse (visible light, 800 or 400 nm) and are then photoejected by the probe pulse (XUV radiation, 30 nm). By varying the time delay between the two pulses, the temporal evolution of the excited carriers can be measured. The investigation of this effect yields information about the dynamics of the unoccupied states, for example electron lifetimes, decay channels or (quasi)particle interactions.
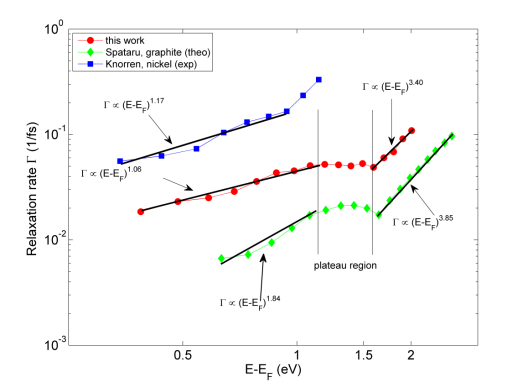
Figure c shows the measured relaxation rates Γ = τ-1 of a graphene / Ni(111) sample as a function of the kinetic energy of the photoelectrons. All measurements have been performed in normal emission. Three distinct regions can be identified: The low energy regime, E-EF < 1 eV, where the measured scattering rates show a strongly metallic behavior similar to measurements performed on pure Ni(111) [7]. Between 1 eV and 1.5 eV a plateau with constant relaxation rates can be seen, similar to those observed in graphite [8]. Above 1.5 eV the relaxation rates increase dramatically, which could also been observed in a calculation for pure graphite [9]. These effects have been attributed to a hybridization of the graphene and Nickel bands. At 1 eV above the Fermi level a saddle point in the electronic band structure between the M and K points of the Brillouin zone leads to constant lifetimes (van-Hove singularity in the density of states). Below 1 eV the contribution from the Ni states dominate, while above 1.5 eV the electronic structure is influenced by strongly carbon-like states [10].
At the same time our set-up offers the option of performing static one-photon photoemission experiments (1PPE) with multiple harmonic orders. A toroidal grating monochromator can be utilized to spatially separate and select a single harmonic over a wide range of harmonic orders
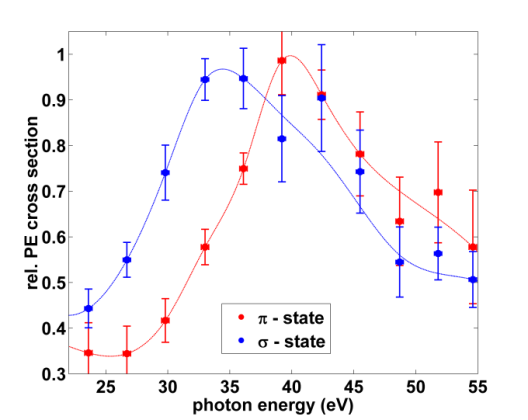
Figure d shows a static 1PPE measurement performed on a graphene/Ni(111) sample. Multiple spectra have been recorded at normal incidence with different photon energies. The relative photoemission cross section has been calculated by measuring the relative π and σ state photoemission intensity as a function of the photon energy. Both show a distinct resonance at 39 and 34 eV respectively. This effect has been attributed to a particularly high density of unoccupied states at these energetic positions above the Fermi level. It could be shown that the shape of the resonance can be reproduced almost exactly by calculating the photoemission cross section from a DFT calculation of the graphene band structure [11].
Cooperations:
- P. Rudolf, University of Groningen, The Netherlands
- S. Forti, K. Emtsev, U. Starke, Max-Planck-Institute for Solid State Physics, Stuttgart, Germany
- T. Winzer, E. Malic, A. Knorr, Institute for Theoretical Physics, TU Berlin, Germany
This work is supported and funded by the Graphene SPP 1459 of the German Research Foundation (DFG).
References:
[1] K. Novoselov et al., Science 306, 666 (2004)
[2] J. Dawlaty et al., Appl. Phys. Lett. 93, 131905 (2008)
[3] C. Lee et al., Science 321, 385 (2008)
[4] Y. Zhang et al., Nature 438, 201 (2005)
[5] K. I Bolotin et al., Solid State Comm. 146, 351 (2008)
[6] Y.-M. Lin et al., Science 327, 662 (2010)
[7] R. Knorren et al., Phys. Rev. B. 61, 9427 (2000)
[8] G. Moos et al., Phys. Rev. Lett. 87, 267402 (2001)
[9] C. D. Spataru et al., Phys. Rev. Lett. 87, 246405 (2001)
[10] L. Bignardi et al., Phys. Rev. B. 89, 075405 (2014)
[11] T. Haarlammert et al., Eur. Phys. J. B 86, 225 (2013)


