Singular Optics

In modern optics, singular optics forms an independent, aspiring field of research, in which the fundamental topological properties of electromagnetic waves – singularities in phase and polarization – are investigated. Scalar phase singularities appear in the center of optical phase vortices in spatially structured light, where they represent dislocation of undefined phase going along with vanishing intensity.

A relatively young field of research is the investigation of polarization singularities, which have attracted growing interest within the last years. Polarization singularities can be naturally observed in e.g. the blue daylight sky caused by Rayleigh scattering of sunlight in the atmosphere. Moreover, they occur in polarization structured light fields, so called Poincaré beams. Different kinds of polarization singularities exist as V-Points, C-Points/Lines, or L-Points/Lines [Otte2015, Alpmann2016], in which the polarization itself, its orientation, or its handedness and ellipticity, respectively, is undefined. We investigate both, phase as well as polarization singularities and their properties.

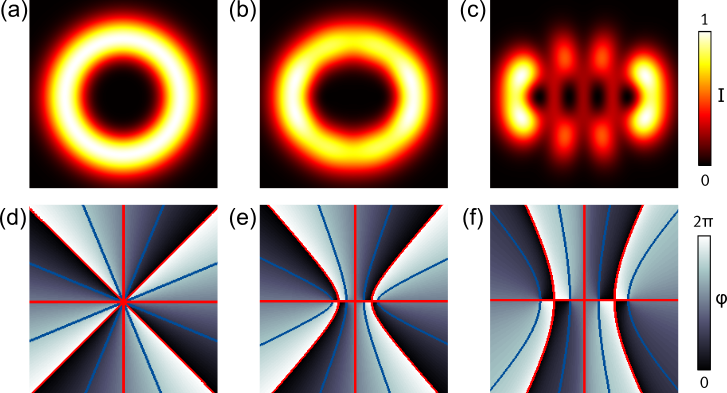
Higher-order standard Gaussian modes: Intensity I and phase φ of a helical (a, d) Laguerre-Gaussian beam, (b, e) and (c,f) Ince-Gaussian beams with an ellipticity ε=5 and 25, respectively. In (d-f) phase singularities are located at crossings of blue (|A|⋅cos⁡(φ)=0) and red (|A|⋅sin⁡(φ)=0) zerolines for E=|A|⋅exp⁡(iφ).

By tailoring sophisticated scalar light fields, i.e. modulate amplitude and phase as desired [Woerdemann2013, Alpmann2015, Diebel2016], the architecture of phase within the beams’ transverse plane can be structured artificially, so that phase singularities of predefined characteristics are generated. Higher-order helical Gaussian modes such as Laguerre or Ince Gaussian beams naturally contain singularities (see Figure above): these beams reveal an azimuthally varying phase distribution within their transverse plane such that phase singularities arouse in their center. With respect to optical trapping, suchlike singularities and the surrounding phase distribution are of particular interest, since realized light fields make trapped particle orbit around singularities (s. video).

Furthermore, we focus on the investigation of polarization singularities: Due to our holographic method of beam shaping […alpmann2016…, Otte2015], we are able to realize polarization structured light fields (vectorial Poincaré beams) containing corresponding singularities. Moreover, we can predefine singularities’ kind, order, number, and position by this technique, facilitating customized Poincaré beams. We analyze singularities in any kind of Poincaré beams within the transverse plane, as well as regarding their longitudinal evolution. For example, we introduced novel hybrid structures [Otte2016] of flowers- and spider-web-like vector fields, exploring the fundamentals of singular optics.

References:

  • [Woerdemann2013] Woerdemann M, Alpmann C, Esseling M and Denz C 2013 “Advanced optical trapping by complex beam shaping” Laser & Photonics Reviews 7(6) 839-854
  • [Alpmann2015] Alpmann C, Schöler C and Denz C 2015 “Elegant Gaussian beams for enhanced optical manipulation” Applied Physics Letters 106(24) 241102
  • [Diebel2016] Diebel F, Boguslawski M, Dadalyan T, Drampyan R, and Denz C 2016 “Controlled soliton formation in tailored Bessel photonic lattices” Optics Express 24(12) 12933
  • [Otte2015] Otte E, Schlickriede C, Alpmann C and Denz C 2015 “Complex light fields enter a new dimension: holographic modulation of polarization in addition to amplitude and phase” Proceedings of SPIE vol. 9379, 937908
  • [Alpmann2016] Alpmann C, Schlickriede C, Otte E and Denz C 2016 “Dynamic modulation of Poincaré beams” submitted
  • [Otte2016] Otte E, Alpmann C, and Denz C 2016 “Higher-order polarization singularities in tailored vector beams” Journal of Optics 18 074012