next up previous contents
Next: A numerical example Up: Prior mixtures Previous: High and low temperature   Contents

Equal covariances

Especially interesting are $j$-independent ${\bf K}_j(\theta)$ = ${\bf K}_0 (\theta )$ with $\theta$-independent determinants so $\det {\bf K}_j$ or $\det \widetilde {\bf K}_j$, respectively, do not have to be calculated.

Notice that this still allows completely arbitrary parameterisations of $t_j(\theta)$. Thus, the template function can for example be a parameterised model, e.g., a neural network or decision tree, and maximising the posterior with respect to $\theta$ corresponds to training that model. In such cases the prior term forces the maximum posterior solution $h$ to be similar (as defined by ${\bf K_0}$) to this trained parameterised reference model.

The condition of invariant $\det{\bf K}_0(\theta)$ does not exclude adaption of covariances. For example, transformations for real, symmetric positive definite ${\bf K}_0 (\theta )$ leaving determinant and eigenvalues (but not eigenvectors) invariant are of the form ${\bf K}(\theta_0)\rightarrow {\bf K}(\theta)= {\bf O}(\theta){\bf K}{\bf O}^{-1}(\theta)$ with real, orthogonal ${\bf O}^{-1}$ = ${\bf O}^{T}$. This allows for example to adapt the sensible directions of multidimensional Gaussians. A second kind of transformations changing eigenvalues but not eigenvectors and determinant is of the form ${\bf K}(\theta_0) = {\bf O}{\bf D}(\theta_0){\bf O}^{T}$ $\rightarrow {\bf K}(\theta) = {\bf O}{\bf D}(\theta){\bf O}^{T}$ if the product of eigenvalues of the real, diagonal ${\bf D}(\theta_0) $ and ${\bf D}(\theta)$ are equal.

Eqs.(29,35) show that the high temperature solution becomes a linear combination of the (potential) low temperature solutions

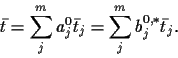\begin{displaymath} \bar t = \sum_j^m a^0_j \bar t_j = \sum_j^m b^{0,*}_j \bar t_j . \end{displaymath} (41)

Similarly, Eq.(21) simplifies to
\begin{displaymath} h =\sum_j^m a_j \bar t_j =\bar t + \sum_j^m (a_j-a_j^0) \, \bar t_j , \end{displaymath} (42)

and Eq.(23) to
\begin{displaymath} a_j= \frac{e^{-\frac{\beta}{2}a {B}_j a-\widetilde E_j}} {\... ...2}a {B}_j a}} {\sum_k b_k\, e^{-\frac{\beta}{2} a {B}_k a}} , \end{displaymath} (43)

introducing vector $a$ with components $a_j$, $m\times m$ matrices $B_j$ defined in (39). Eq.(42) is still a nonlinear equation for $h$, it shows however that the solutions must be convex combinations of the $h$-independent $\bar t_j$ (see Fig. 2). Thus, it is sufficient to solve Eq.(43) for $m$ mixture coefficients $a_j$ instead of Eq.(21) for the function $h$.

Figure 2: Left: Example of a solution space for $m$ = 3. Shown are three low temperature solutions $\bar t_j$, high temperature solution $\bar t$, and a possible solution $h$ at finite $\beta $. Right: Exact $b_1$ vs. (dominant) $a_1$ (dashed) for $m$ = $2$, $b$ = 2, $\widetilde E_1$ = 0.405, $\widetilde E_2$ = 0.605.
\begin{figure}\begin{center} \setlength{\unitlength}{0.57mm}\begin{picture}(44,3... ...0.2cm} \epsfig{file=cmp.eps, width=37mm}\end{center}\vspace{-0.5cm} \end{figure}

Figure 3: Shown are the plots of $f_1(a_1)=a_1$ and $f_2(a_1)=\frac{1}{2} \left(\tanh \Delta + 1\right)$ within the inverse temperature range $0\le \beta \le 4$ (for $b=2$, $\widetilde E_2-\widetilde E_1$ = $0.1\beta $). Notice the appearance of a second stable solution at low temperatures.
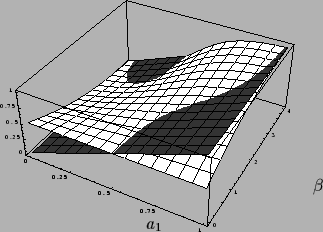\begin{figure}\vspace{-1.5cm} \begin{center} $\!\!\!\!\!\!\!\!\!\!$\epsfig{file=... ... \put(273,110){\makebox(0,0){$\beta$}} \end{picture}\vspace{-2.7cm} \end{figure}

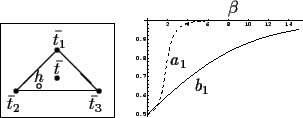
For two prior components, i.e., $m=2$, Eq.(42) becomes

\begin{displaymath} h =\frac{\bar t_1 + \bar t_2}{2} + \left(\tanh \Delta\right) \frac{\bar t_1 - \bar t_2}{2} , \end{displaymath} (44)

with
\begin{displaymath} \Delta = \frac{E_2-E_1}{2} = \frac{\beta}{4} \,b(2 a_1-1) + \frac{\widetilde E_2-\widetilde E_1}{2} , \end{displaymath} (45)

because the matrices $B_j$ are in this case zero except $B_1(2,2) = B_2(1,1) = b$. For $E_{\theta,\beta,j}$ uniform in $j$ we have $(\bar t_1+\bar t_2)/2$ = $\bar t$ so that $a_j^0$ = $0.5$. The stationarity Eq.(43), being analogous to the celebrated mean field equation of a ferromagnet, can be solved graphically (see Fig.3 and Fig.2 for a comparison with $b_j$), the solution is given by the point where
\begin{displaymath} a_1 = \frac{1}{2} \left(\tanh \Delta + 1\right) . \end{displaymath} (46)

next up previous contents
Next: A numerical example Up: Prior mixtures Previous: High and low temperature   Contents
Joerg_Lemm 1999-12-21