



Next: High and low temperature
Up: Prior mixtures
Previous: Maximum a posteriori approximation
Contents
The optimal regression function under squared-error loss
-- for Gaussian regression identical to the log-loss
of density estimation --
is the predictive mean.
For mixture model (12)
one finds, say for fixed  ,
,
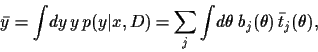 |
(27) |
with
mixture coefficients
The component means 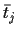 and
the likelihood of
and
the likelihood of 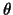 can be calculated analytically
[17,14]
can be calculated analytically
[17,14]
and
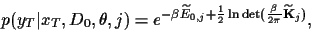 |
(30) |
where
and
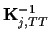 is the projection
of the covariance
is the projection
of the covariance
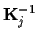 into the
into the
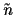 -dimensional space
for which training data are available.
(
-dimensional space
for which training data are available.
(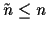 is the number of data with distinct
is the number of data with distinct
 -values.)
-values.)
The stationarity equation
for a maximum a posteriori approximation
with respect to 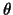 is at this stage found from
(28,30)
is at this stage found from
(28,30)
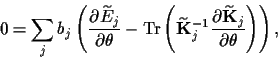 |
(33) |
where
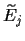 =
=
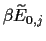 +
+
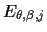 .
Notice that Eq.(33)
differs from Eq.(22)
and requires only to deal with
the
.
Notice that Eq.(33)
differs from Eq.(22)
and requires only to deal with
the
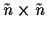 -matrix
-matrix
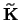 .
The coefficient
.
The coefficient
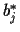 =
= 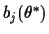 for
for 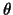 set to its maximum posterior value
is of form
(23)
with the replacements
set to its maximum posterior value
is of form
(23)
with the replacements
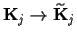 ,
,
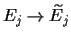 .
.




Next: High and low temperature
Up: Prior mixtures
Previous: Maximum a posteriori approximation
Contents
Joerg_Lemm
1999-12-21
![]() ,
,
![]() is at this stage found from
(28,30)
is at this stage found from
(28,30)