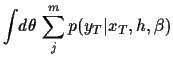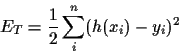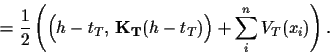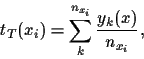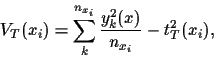Next: Maximum a posteriori approximation
Up: Prior mixtures
Previous: Prior mixtures
Contents
Decomposed into components
the posterior density becomes
Writing probabilities in terms of energies,
including parameter dependent normalisation factors
and skipping parameter independent factors yields
This defines
hyperprior energies
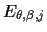 ,
prior energies
,
prior energies 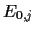 (`quadratic concepts')
(`quadratic concepts')
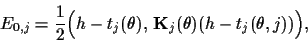 |
(14) |
(the generalisation
to a sum of quadratic terms
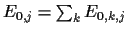 is straightforward)
and
training or likelihood energy (training error)
is straightforward)
and
training or likelihood energy (training error)
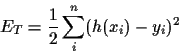 |
(15) |
The second line is a
`bias-variance' decomposition
where
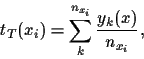 |
(16) |
is the mean of the 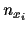 training data available for
training data available for 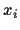 ,
and
,
and
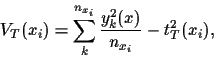 |
(17) |
is the variance of 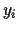 values at
values at 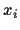 .
(
.
(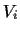 vanishes if every
vanishes if every 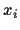 appears only once.)
The diagonal matrix
appears only once.)
The diagonal matrix 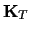 is
restricted to the space of
is
restricted to the space of  for which
training data are available and has matrix elements
for which
training data are available and has matrix elements 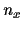 .
.




Next: Maximum a posteriori approximation
Up: Prior mixtures
Previous: Prior mixtures
Contents
Joerg_Lemm
1999-12-21