High-order Harmonic Generation
With the advent of ultrashort pulsed laser sources time resolved ultraviolet photoelectron spectroscopy (TR-UPS) has become one of the most advanced tools to investigate femtosecond electron dynamics in solid and gaseous systems. However, many pulsed light sources, like the common Titanium:Sapphire laser (Ti:Sa), emit light in the visible or infrared spectral range. In order to access more tightly bound electronic states or the outer areas of the Brillouin zone in a solid sample higher photon energies would be more suitable. The frequency conversion through High-order Harmonics allows the generation of radiation in the extreme ultraviolet (XUV) and soft x-ray regime without increasing the pulse duration1. Another remarkable feature of the High Harmonics is the so-called plateau region, where the photon yield is constant over a large range of photon energies.
A major difficulty is the experimental realization. An extremely intense laser is needed to generate the high harmonics, and because of the short wavelengths an ultrahigh vacuum system (UHV) is required to avoid absorption in air.
Generation principle
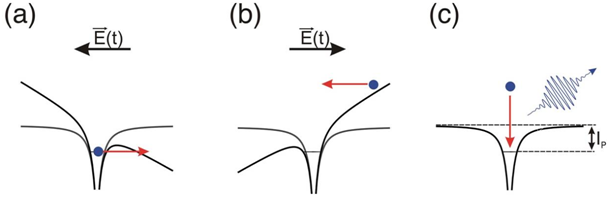
Fig. 1: Three step model. (a) Tunneling, (b) Acceleration, (c) Recombination
The intense pulses of a femtosecond Ti:Sa laser (I > 1014 W/cm²) are focussed in an open gas cell filled with a rare gas, most commonly argon, neon or helium. Through a nonlinear interaction of the intense laser field with the gas odd multiples of the fundamental light (800 nm) are generated simultaneously, the so called High Harmonics. The generation process can be described by a semi-classical three step model2,3 (see fig. 1):
- Step 1, Tunneling: The electron is bound by the Coulomb potential of an atom. An incoming intense laser field distorts the potential and allows the tunneling of the electron through the Coulomb barrier.
- Step 2, Acceleration: The free electron is accelerated away from its parent ion by the laser field. After half an optical cycle the sign of the laser field reverses, this leads to an acceleration back towards the ion.
- Step 3, Recombination: The electron recombines with its parent ion and emits a photon with a photon energy composed of the ionization energy of the atom IP and the kinetic energy of the electron gained by its interaction with the laser field. Only photons with a photon energy of integer multiples of the fundamental photon energy are generated. Due to interference effects the even numbered harmonics are erased, only odd numbered harmonics survive. The maximum photon energy (cut-off) is given by Emax = IP + 3.17 UP, with UP the ponderomotive potential of the laser field.
Interaction volume
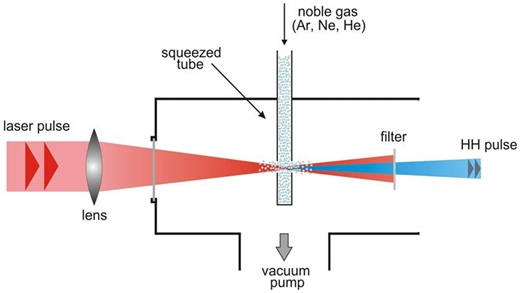
Fig. 2: Generation of High Harmonics in a squeezed tube
The interaction volume consists of a squeezed steel tube filled with a noble gas with a backing pressure of about 200 mbar. An open ended gas cell is formed by the laser itself, which drills a hole through the metal. The gas then exhausts into the surrounding vaccum.
To separate the simultaneously generated harmonics two monochromators can be utilized. Through diffraction on a toroidal grating the harmonics can be separated spatially and can be selected by rotating the grating. The grating also serves as a focussing mirror with low astigmatism. The diffraction however leads to a puls front tilt, which is equivalent to a prolonged pulse duration. To avoid this effect for time resolved experiments a mirror monochromator can be utilized, which consists of two multilayer Si-Mo mirrors, optimized to reflect one harmonic and absorbing all others. In the present case the monochromator is optimized for the 25th harmonic.
High Harmonic Spectra
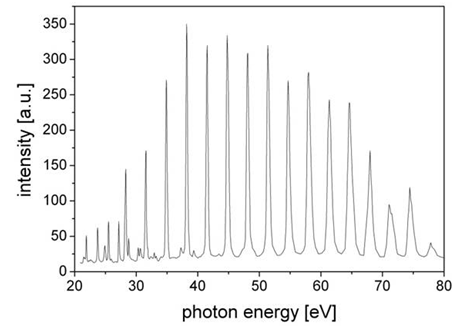
Fig. 3: Sample spectrum of High Harmonics, generated in Neon
Figure 3 shows a sample spectrum of high harmonics, generated in a Neon gas cell. The plateau region is clearly visible, the lower photon yields below 30 eV and above 70 eV are not caused by the cut-off but rather by the limited transmission of an additional aluminium filter used to block out the fundamental beam. The highest conversion efficiency is reached at the 25th harmonic (39.2 eV).
1 F. Krausz, M. Ivanov, Review of Modern Physics 81, 163 (2009)
2 P. B. Corkum, Phys. Rev. Lett. 71, 1994–1997 (1993)
3 M. Schnürer et al., Phys. Rev. Lett. 80, 3236 (1998)


