Research interests - Prof. Dr. Michael Rohlfing
Already in the electronic ground state, there is a delicate balance between the nuclei, electrons, electrostatics, and quantum mechanics. For many systems, density-functional theory (DFT) allows to treat the quantum mechanics of the many-electron system, to energy-optimize the geometry, and to understand details of chemical bonding.

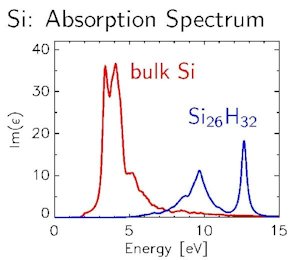
Optical spectra (continous spectra, excitons, charge-transfer states, and localized states like self-trapped excitons) are heavily influenced by electronic correlation, as well, in particular by electron-hole interaction effects. Such issues are important both for the characterization of systems, as well as for applications like optielectronics or photovoltaics.
Since the electronic structure deoends on the atom positions, it is not surprising that the atom positions depend on the electronic structure, as well. In particular, the geometry may change if the electronic structure is excited. A number of consequences arise, like vibrational broadening of electronic transitions, Stokes shifts between light absorption and emission, self trapping of excitons, and fragmentation of the system.

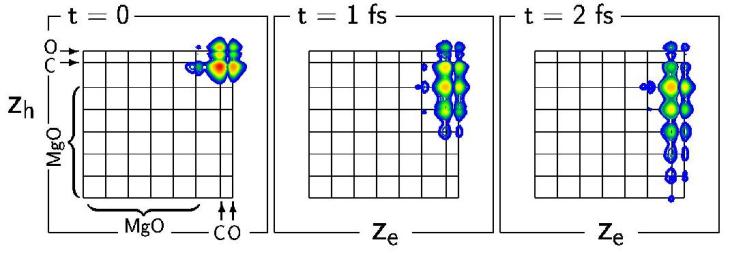
Excitations often happen via states that are not eigenstates of the electronicstructure, thus giving rise to state propagation in time which typically happens on a femtosecond time scale. Two prominent examples are resonant charge transfer processes (e.g., from an adsorbate to the substrate) and decay mechanisms dueto the finite lifetime of electronic states resulting from electron-electron interaction.
In experiment, very detailed information about geometric and electronic structures can be obtained from scanning-tunneling microscopy (STM). The simulation ofSTM images is thus an important tool at the interface between theory and experiment.
The spectral properties of a many-electron system are determined by transitionsbetween its ground state and the excited states. For the problems we have in mind two classes of excited states are relevant: states with an electron number changing by plus/minus 1 (i.e., hole-like and electron-like excitations, whose energies define the band structure), as well as excited states without changing thenumber of electrons (in particular, electron-hole pairs that are relevant for optical excitations). Correspondingly, the mathematical description and its numerical realization of these concepts on powerful computer platforms is carried outin several consecutive steps.