Nonlinear effects

Nonlinear effects play an important role in modern photonics. By light-matter interaction, it becomes possible to selectively influence optical properties of materials with light. These changes then directly affect the propagation of the light itself. This allows future concepts for "Light controls light".

The phenomenon of self-focusing of light has attracted huge attention in the field of nonlinear optics in the past. While localized light fields broaden during their linear propagation due to diffraction, nonlinear effects can focus the beam and compensate the diffraction. If the beam diffraction and the nonlinear self-focusing are exactly balanced, nonlinearly localized structures can from, so-called optical solitons. They are characterized by a stable propagation with unchanged field distribution.

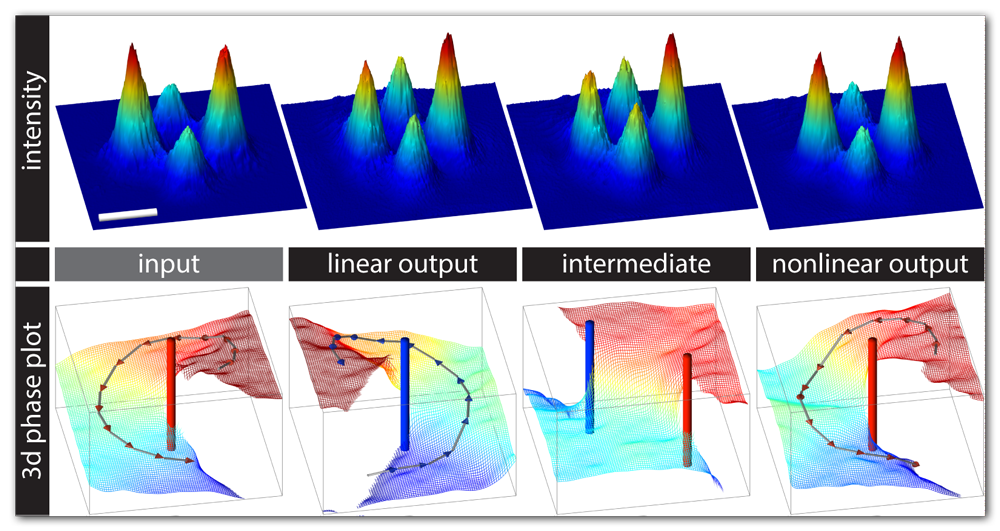
Combining nonlinearity and photonic lattices enables a whole variety of new opportunities for all-optical control and switching of light [1,2]. For example, this way it is possible to realize an intensity-dependent binary switch for the topological charge of an optical vortex inside a two-dimensional structure of four coupled nonlinear waveguides [3] (see Fig. 1). At low intensities, the charge of an incoming discrete vortex is flipped, while at high intensities it remains and forms a so-called vortex soliton [4].

While studying nonlinear effects the formation of solitons, one is not limited to a particular configuration of optical waveguides. Rather, a variety of photonic lattices supports solitons with fascinating spatiotemporal properties. In a two-dimensional photonic lattice with parabolic refractive index modulation stable spatial solitons can be realized that perform a spatial oscillation during propagation [5].

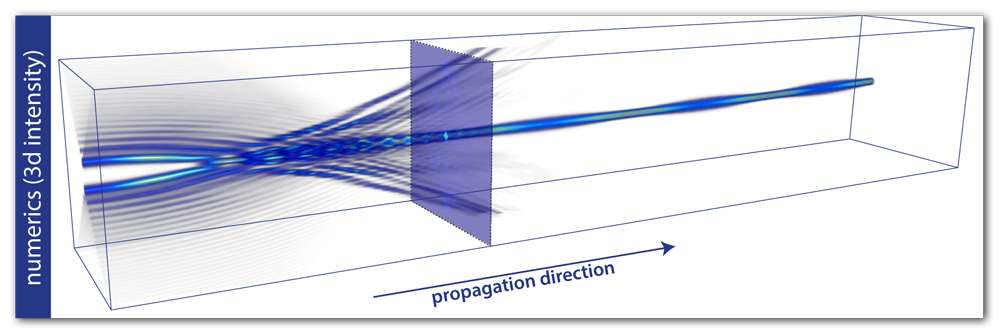
Moreover, the fascinating class of [accelerated beams] can be combined with nonlinearity and this way the interaction between acceleration beams and nonlinear self-focusing can be studied. The example of nonlinear interaction multiple two dimensional Airy beams shows that the acceleration together with the nonlinearity leads to the formation of spatial solitons or soliton-pairs [6]. The nonlinearity allows that the Airy beams interact with each other and can mutually compensate their accelerations (see Fig. 2).

References:
[1]     F. Lederer, et al., “Discrete solitons in optics,” Phys. Rep. 463, 1 (2008)
[2]     P. Rose, M. Boguslawski, and C. Denz, “Nonlinear lattice structures based on families of complex nondiffracting beams,” New J. Phys. 14, 033018 (2012).
[3]     F. Diebel, C. Denz, et al., “All-optical switching in optically induced nonlinear waveguide couplers All-optical switching in optically induced nonlinear waveguide couplers,” Appl. Phys. Lett. 104, 261111 (2014).
[4]     B. Terhalle, C. Denz, et al. „Observation of Multivortex Solitons in Photonic Lattices,” Phys. Rev. Lett. 101, 013903 (2008).
[5]     F. Diebel, P. Rose, M. Boguslawski, and C. Denz, “Observation of spatially oscillating solitons in photonic lattices;” New J. Phys. 18, 053038 (2016).
[6]     F. Diebel, C. Denz, et al., “Soliton formation by decelerating interacting Airy beams,” Opt. Express 23, 24351 (2015).