Topology

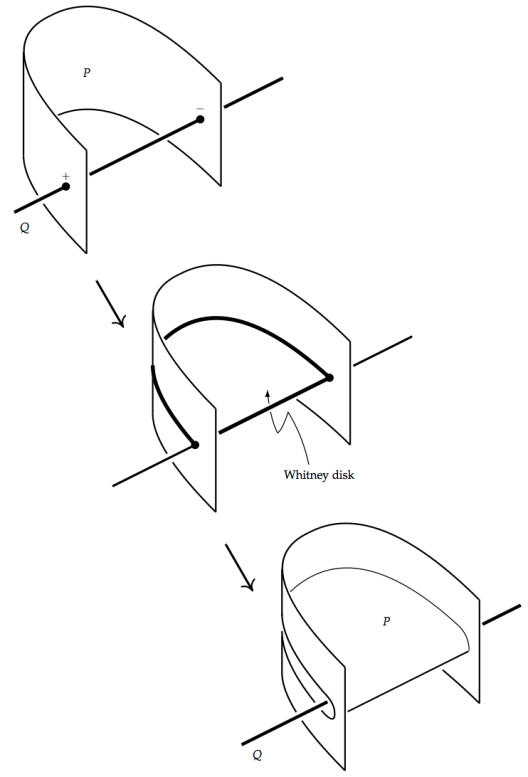
''The Whitney-Trick''. Taken from Scorpan, Alexandru. The Wild World of 4-Manifolds. Providence: American Mathematical Society, 2005, Figure 1.26, S.46, with the consent of the AMS.
© AMS

The subject matter of topology are discrete invariants of topological spaces (for example smooth manifolds) and maps between them. The simplest such invariant is the winding number of a curve in the plane. One of the principal goals is to study whether a manifold is uniquely determined by its discrete invariants. Of particular interest in the focus subject are stable homotopy theory, K-theory, differential topology, index theory and geometric group theory.

Topology is not an isolated discipline, but has intense connections to other areas of theoretical mathematics, such as algebra, differential geometry, geometric group theory and the theory of operator algebras.

Prerequisites

Prerequisites for the specialization in topology are the lecture courses ''Foundations of analysis, topology and geometry'' and ''Topology I'' (or equivalent courses), with the following contents:

  • Topology I: singular homology theory, CW complexes and cellular homology, the cross product and the Künneth theorem.
  • Foundations of analysis, topology and geometry: notions of point set topology, fundamental group and covering spaces, smooth manifolds.

 

This page presents the plan at the time of writing for the courses in future semesters. Please note that this plan is subject to change, and courses may be dropped, added, or modified in reaction to currently unforeseen events.

Courses for the specialisation in Topology

Winter semester 2024/2025

apl. Prof. Dr. Michael Joachim: Topology 3 (Type I, II)

Summer semester 2024

Prof. Dr. Johannes Ebert: Homotopy Theory II (Type II)

Winter semester 2023/2024

Prof. Dr. Johannes Ebert: Homotopy Theory

Summer semester 2023

Prof. Dr. Michael Weiss: Topology IV

Winter semester 2022/23

Dr. Martin Bays: Geometric Group Theory I (Type II)
Prof. Dr. Michael Weiss: Topology III (Type I, II)