Aperiodische deterministische & zufällige photonische Strukturen

Systeme höchster Ordnung und Symmetrie, bspw. hochperiodische Gitter, sind nicht der Normalfall in der Natur - Unordnung ist omnipräsent. Dementsprechend werden physialische Modelle gebraucht, die Systeme in Unordnung möglichst genau beschreiben. Zum einen begegnet man der Goldene Zahl, der irrationalsten Zahl überhaupt, in verschiedensten Bereichen, bspw. in der Natur (Phyllotaxis von Pflanzen, Planetenumlaufbahnen) oder in der Kunst (Musik, Architektur, Malerei). Andererseits ist der Einbruch der Leitfähigkeit in Festkörpern auf Wellenlokalisierung zurückzuführen. Generell erlaubt die Allgemeingültigkeit von Wellenphänomenen die in der Optik anhand von Lichtwellenausbreitung gewonnenen Erkenntnisse auf andere Systeme zu übertragen.

Nichtbeugende Strahlen bieten auf makroskopischen Propagationslängen eine konstant bleibende, mikroskopische Modulation der Intensität. Wir nutzen diese Lichtformen, um den Brechungsindex photorefraktiver Kristalle künstlich in Unordnung zu versetzen. Die daraus hervorgehenden Anordnungen entsprechen zweidimensionalen Wellenmedien. Da Schreib-, Propagations- und Löschprozesse direkt in situ passieren und zusätzliches Präparieren der Probe nicht nötig ist, sind umfangreiche Ensembles ähnlicher Lichtpotentiale sehr leicht herzustellen. Aussagekräftige statistische Erhebungen werden so erst möglich.

Sogenannte Vogel-Spiralen sind typische Vertreter aperiodischer Strukturen, die Phyllotaxis von Pflanzen nachbilden. Die Realisierung derartiger und anderer quasiperiodischer als auch aperiodischer Strukturen erlaubt eine detaillierte Untersuchung von Transportvorgängen in Anordnungen fernab von Periodizität. Dieser Motivation folgend erzeugen wir auch sogenannte deterministische aperiodische Strukturen (DAS). Derartige Gitter bestehen bspw. aus einer zweidimensionalen Kombination zweier binärer Fibonacci-Sequenzen und sind bekannt für ihre sehr heterogenen, lokal stark variierenden Wellentransporteigenschaften. Trotz der - bezogen auf periodische Gitter - nur leicht herabgesetzten Ordnung findet man bereits in Fibonacci-Gittern eine reduzierte Transportfähigkeit. Es existieren jedoch zahlreiche DAS-Realisierungen, deren Grad an Ordnung ein breites Spektrum abdeckt. Ein Übergang von geordneten zu ungeordneten Strukturen ist damit natürlich gegeben.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

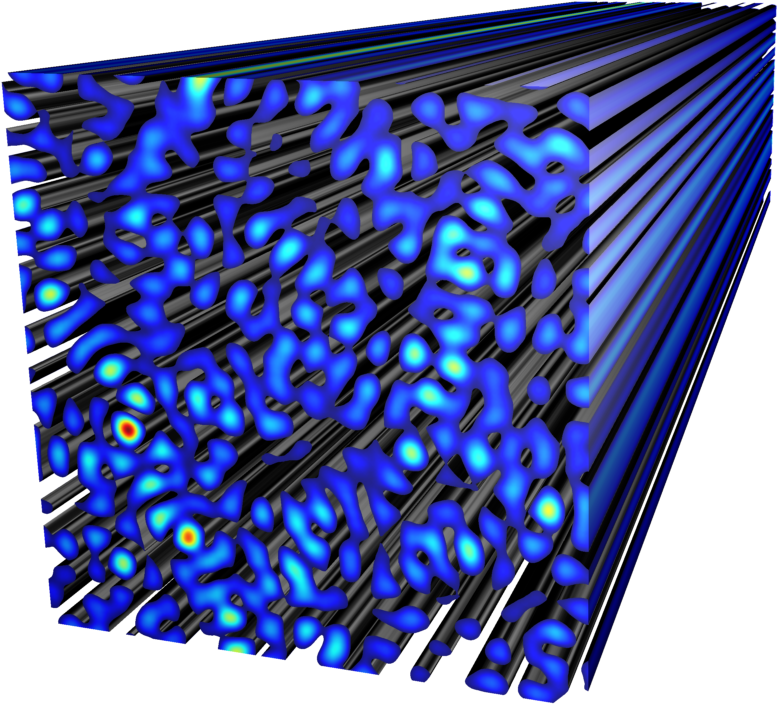
Desweiteren beschäftigen wir uns mit der Erzeugung vollständig zufälliger photonischer Systeme. Diese bieten eine geeignete Plattform zur Untersuchung von Anderson-Lokalisierung und kohärenter Rückstreuung. Beides sind verwandte Wellenphänomene, die auf besondere Interferenzbedingungen in mehrfachstreuenden Medien zurückzuführen sind. Mit unserer experimentellen Umsetzung erzielen wir tiefe Einblicke in die Physik dieser faszinierenden Systeme. Beispielsweise konnten wir die Stärke der Unordnung und die photonische Korngröße als Parameter identifizieren, die entscheidenden Einfluss auf die Lichtleitfähigkeit haben.

In stark streuenden Medien kommt es nahe der Lichteinkopplung zu konstruktiver Interferenz. In Zusammenhang mit Anderson-Lokalisierung spricht man daher auch von starker Lokalisierung. Im Gegensatz dazu findet man im schwach streuenden Regime spektral einen dominanten konstruktiven Interferenzbeitrag, dessen räumliche Frequenz dem invertierten Wellenvektor der Eingangswelle entspricht. Die Bezeichnung kohärente Rückstreuung synonym zur schwachen Lokalisierung ist daher naheliegend.