



Next: Analytical solution of mixture
Up: Prior mixtures for regression
Previous: High and low temperature
Contents
Especially interesting is the case
of 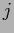 -independent
-independent
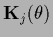 =
=
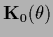 and
and 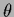 -independent
-independent
 .
In that case the often difficult to obtain
determinants of
.
In that case the often difficult to obtain
determinants of 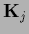 do not have to be calculated.
do not have to be calculated.
For 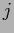 -independent inverse covariances
the high temperature solution
is
according to
Eqs.(555,561)
a linear combination
of the (potential) low temperature solutions
-independent inverse covariances
the high temperature solution
is
according to
Eqs.(555,561)
a linear combination
of the (potential) low temperature solutions
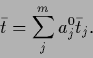 |
(566) |
It is worth to emphasize that, as the solution
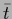 is not a mixture of the component templates
is not a mixture of the component templates 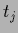 but of component solutions
but of component solutions 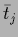 ,
even poor choices for the template functions
,
even poor choices for the template functions 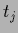 can lead to good solutions, if enough data are available.
That is indeed the reason why the most common choice
can lead to good solutions, if enough data are available.
That is indeed the reason why the most common choice 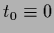 for a Gaussian prior can be successful.
for a Gaussian prior can be successful.
Eqs.(565) simplifies to
 |
(567) |
where
 |
(568) |
and (for  -independent
-independent  )
)
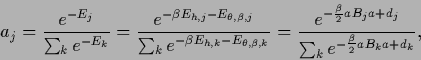 |
(569) |
introducing
vector 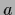 with components
with components 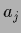 ,
,
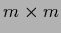 matrices
matrices
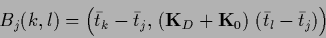 |
(570) |
and constants
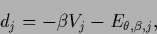 |
(571) |
with 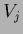 given in (564).
Eq. (567) is still a nonlinear equation
for
given in (564).
Eq. (567) is still a nonlinear equation
for  , it shows however that the solutions
must be convex combinations of the
, it shows however that the solutions
must be convex combinations of the  -independent
-independent 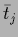 .
Thus, it is sufficient to solve
Eq. (569) for
.
Thus, it is sufficient to solve
Eq. (569) for 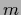 mixture coefficients
mixture coefficients 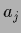 instead of Eq. (548) for the function
instead of Eq. (548) for the function  .
.
The high temperature relation
Eq. (553) becomes
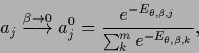 |
(572) |
or 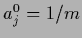 for a hyperprior
for a hyperprior
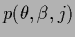 uniform with respect to
uniform with respect to 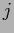 .
The low temperature relation Eq. (559)
remains unchanged.
.
The low temperature relation Eq. (559)
remains unchanged.
For  Eq. (567) becomes
Eq. (567) becomes
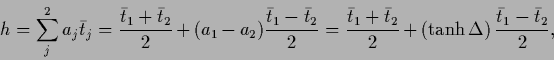 |
(573) |
with
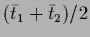 =
= 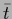 in case
in case
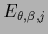 is uniform in
is uniform in 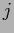 so that
so that 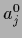 =
=  , and
, and
because
the matrices 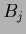 are in this case zero except
are in this case zero except
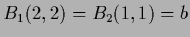 .
The stationarity Eq. (569) can be solved
graphically (see Figs.7, 8),
the solution being given by the point
where
.
The stationarity Eq. (569) can be solved
graphically (see Figs.7, 8),
the solution being given by the point
where
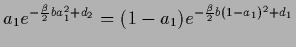 ,
or, alternatively,
,
or, alternatively,
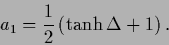 |
(575) |
That equation is analogous to
the celebrated mean field equation of the
ferromagnet.
We conclude that in the case of equal component covariances,
in addition to the linear low-temperature equations,
only a 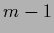 -dimensional nonlinear equation has to be solved
to determine the
`mixing coefficients'
-dimensional nonlinear equation has to be solved
to determine the
`mixing coefficients'
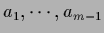 .
.
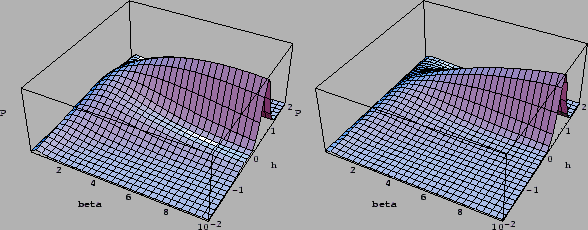
Figure:
The solution of stationary equation
Eq. (569) is given by the point where
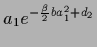 =
=
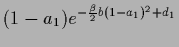 (upper row) or, equivalently,
(upper row) or, equivalently,
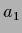 =
=
 (lower row).
Shown are, from left to right, a situation
at high temperature and one stable solution (
(lower row).
Shown are, from left to right, a situation
at high temperature and one stable solution (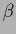 =
= 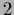 ),
at a temperature (
),
at a temperature (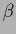 =
= 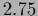 ) near the bifurcation,
and at low temperature with
two stable and one unstable solutions
) near the bifurcation,
and at low temperature with
two stable and one unstable solutions 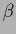 =
= 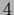 .
The values of
.
The values of 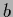 =
= 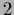 ,
,
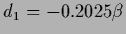 and
and
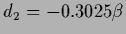 used for the plots
correspond for example to the one-dimensional
model of Fig.9 with
used for the plots
correspond for example to the one-dimensional
model of Fig.9 with 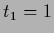 ,
, 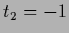 ,
, 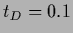 .
Notice, however, that the shown relation is valid
for
.
Notice, however, that the shown relation is valid
for  at arbitrary dimension.
at arbitrary dimension.
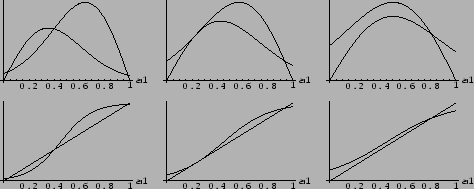 |
Figure 8:
As in Fig.7
the plots of 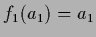 and
and
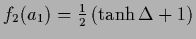 are shown
within the inverse temperature range
are shown
within the inverse temperature range
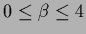 .
.
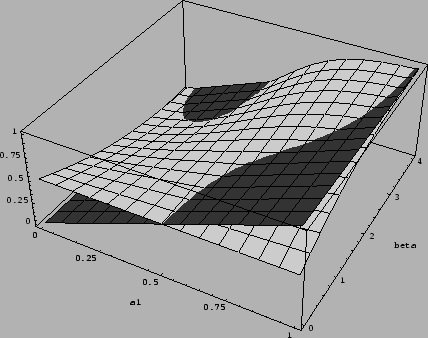 |
Figure 9:
Shown is the joint posterior density of 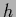 and
and 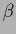 , i.e.,
, i.e.,
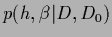
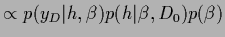 for a zero-dimensional example
of a Gaussian prior mixture model
with training data
for a zero-dimensional example
of a Gaussian prior mixture model
with training data 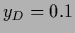 and prior data
and prior data 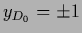 and inverse temperature
and inverse temperature 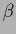 .
L.h.s.:
For uniform prior (middle)
.
L.h.s.:
For uniform prior (middle)
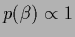 with
joint posterior
with
joint posterior 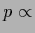
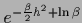
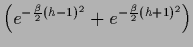 the maximum appears at finite
the maximum appears at finite 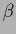 .
(Here no factor
.
(Here no factor 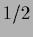 appears in front of
appears in front of 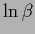 because normalization constants for prior and likelihood term have
to be included.)
R.h.s.:
For compensating hyperprior
because normalization constants for prior and likelihood term have
to be included.)
R.h.s.:
For compensating hyperprior
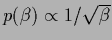 with
with
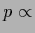
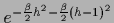
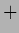
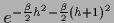 the maximum is at
the maximum is at 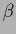 =
=  .
.
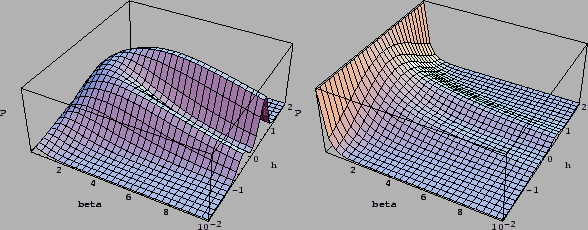 |
Figure 10:
Same zero-dimensional prior mixture model
for uniform hyperprior on  as in Fig.9,
but for varying data
as in Fig.9,
but for varying data
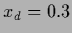 (left),
(left),
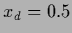 (right).
(right).
 |




Next: Analytical solution of mixture
Up: Prior mixtures for regression
Previous: High and low temperature
Contents
Joerg_Lemm
2001-01-21
![]() -independent
-independent
![]() =
=
![]() and
and ![]() -independent
-independent
![]() .
In that case the often difficult to obtain
determinants of
.
In that case the often difficult to obtain
determinants of ![]() do not have to be calculated.
do not have to be calculated.
![]() -independent inverse covariances
the high temperature solution
is
according to
Eqs.(555,561)
a linear combination
of the (potential) low temperature solutions
-independent inverse covariances
the high temperature solution
is
according to
Eqs.(555,561)
a linear combination
of the (potential) low temperature solutions
![]() Eq. (567) becomes
Eq. (567) becomes
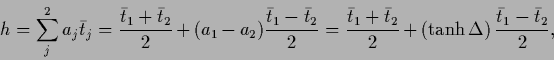
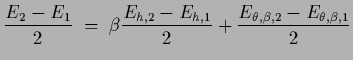
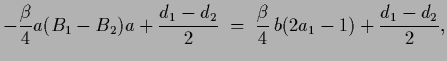
![]() -dimensional nonlinear equation has to be solved
to determine the
`mixing coefficients'
-dimensional nonlinear equation has to be solved
to determine the
`mixing coefficients'
![]() .
.


