Next: Equal covariances
Up: Prior mixtures for regression
Previous: Prior mixtures for regression
Contents
It are the limits of large and small 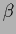 which make the introduction of this additional parameter useful.
The reason being that the high temperature limit
which make the introduction of this additional parameter useful.
The reason being that the high temperature limit
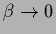 gives the convex case,
and statistical mechanics provides us
with high and low temperature expansions.
Hence, we study the high temperature and low temperature limits
of Eq. (551).
gives the convex case,
and statistical mechanics provides us
with high and low temperature expansions.
Hence, we study the high temperature and low temperature limits
of Eq. (551).
In the high temperature limit
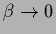 the exponential factors
the exponential factors 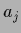 become
become 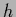 -independent
-independent
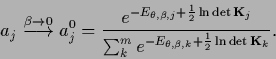 |
(553) |
In case one chooses
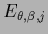 =
=
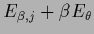 one has to replace
one has to replace
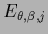 by
by 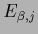 .
The high temperature solution becomes
.
The high temperature solution becomes
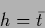 |
(554) |
with (generalized) `complete template average'
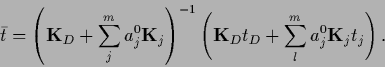 |
(555) |
Notice that 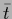 corresponds to the minimum of the quadratic
functional
corresponds to the minimum of the quadratic
functional
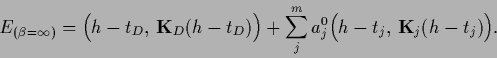 |
(556) |
Thus, in the infinite temperature limit
a combination of quadratic priors by OR is
effectively replaced by a combination by AND.
In the low temperature limit
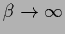 we have,
assuming
we have,
assuming
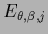 =
=
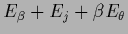 ,
,
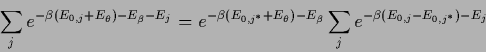 |
(557) |
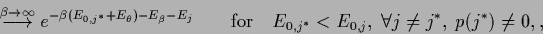 |
(558) |
meaning that
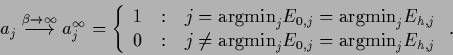 |
(559) |
Henceforth,
all (generalized) `component averages' 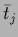 become solutions
become solutions
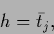 |
(560) |
with
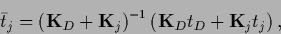 |
(561) |
provided the
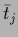 fulfill the stability condition
fulfill the stability condition
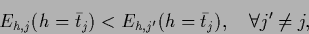 |
(562) |
i.e.,
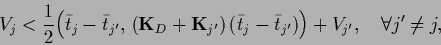 |
(563) |
where
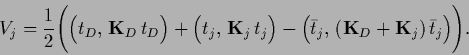 |
(564) |
That means
single components become solutions at zero temperature 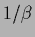 in case their (generalized) `template variance'
in case their (generalized) `template variance' 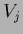 ,
measuring the discrepancy
between data and prior term, is not too large.
Eq. (551)
for
,
measuring the discrepancy
between data and prior term, is not too large.
Eq. (551)
for 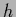 can also be expressed by the
(potential) low temperature solutions
can also be expressed by the
(potential) low temperature solutions 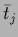
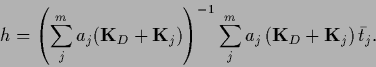 |
(565) |
Summarizing, in the high temperature limit
the stationarity equation (548)
becomes linear with a single solution being essentially
a (generalized) average of all template functions.
In the low temperature limit the single component solutions become stable
provided their (generalized) variance corresponding to their minimal error
is small enough.




Next: Equal covariances
Up: Prior mixtures for regression
Previous: Prior mixtures for regression
Contents
Joerg_Lemm
2001-01-21
![]() which make the introduction of this additional parameter useful.
The reason being that the high temperature limit
which make the introduction of this additional parameter useful.
The reason being that the high temperature limit
![]() gives the convex case,
and statistical mechanics provides us
with high and low temperature expansions.
Hence, we study the high temperature and low temperature limits
of Eq. (551).
gives the convex case,
and statistical mechanics provides us
with high and low temperature expansions.
Hence, we study the high temperature and low temperature limits
of Eq. (551).
![]() the exponential factors
the exponential factors ![]() become
become ![]() -independent
-independent
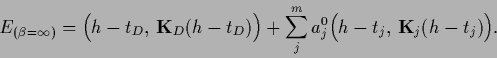
![]() we have,
assuming
we have,
assuming
![]() =
=
![]() ,
,