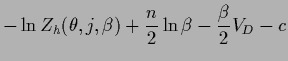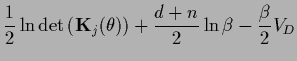Next: High and low temperature
Up: Non-Gaussian prior factors
Previous: Prior mixtures for density
Contents
Prior mixtures for regression
For regression it is especially useful to introduce
an inverse temperature multiplying the terms
depending on 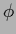 , i.e., likelihood and prior.4As in regression
, i.e., likelihood and prior.4As in regression 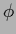 is represented by the regression function
is represented by the regression function 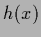 the temperature-dependent error functional becomes
the temperature-dependent error functional becomes
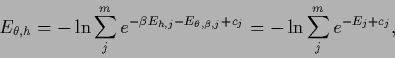 |
(544) |
with
 |
(545) |
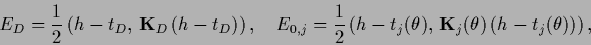 |
(546) |
some hyperprior energy
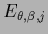 ,
and
,
and
with some constant 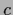 .
If we also maximize with respect to
.
If we also maximize with respect to 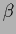 we have to include the (
we have to include the (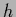 -independent)
training data variance
-independent)
training data variance
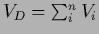 where
where
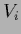 =
=
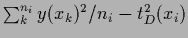 is the variance of the
is the variance of the  training data at
training data at 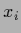 .
In case every
.
In case every 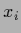 appears only once
appears only once 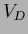 vanishes.
Notice that
vanishes.
Notice that 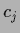 includes a contribution from the
includes a contribution from the 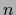 data points
arising from the
data points
arising from the 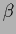 -dependent normalization
of the likelihood term.
Writing the stationarity equation
for the hyperparameter
-dependent normalization
of the likelihood term.
Writing the stationarity equation
for the hyperparameter 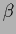 separately,
the corresponding three stationarity conditions
are found as
separately,
the corresponding three stationarity conditions
are found as
As 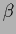 is only a one-dimensional parameter
and its density can be quite non-Gaussian
it is probably most times more informative
to solve for varying values of
is only a one-dimensional parameter
and its density can be quite non-Gaussian
it is probably most times more informative
to solve for varying values of 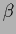 instead to restrict to a single
`optimal'
instead to restrict to a single
`optimal' 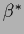 .
Eq. (548)
can also be written
.
Eq. (548)
can also be written
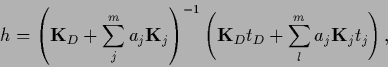 |
(551) |
with
being thus still a nonlinear equation for 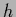 .
.
Subsections




Next: High and low temperature
Up: Non-Gaussian prior factors
Previous: Prior mixtures for density
Contents
Joerg_Lemm
2001-01-21
![]() , i.e., likelihood and prior.4As in regression
, i.e., likelihood and prior.4As in regression ![]() is represented by the regression function
is represented by the regression function ![]() the temperature-dependent error functional becomes
the temperature-dependent error functional becomes