



Next: Additive models
Up: Parameterizing likelihoods: Variational methods
Previous: Linear trial spaces
Contents
Mixture models
The function 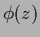 can be approximated by a mixture model,
i.e., by a linear combination of components functions
can be approximated by a mixture model,
i.e., by a linear combination of components functions
 |
(390) |
with parameter vectors 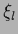 and constants
and constants 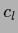 (which could also be included into the vector
(which could also be included into the vector 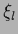 )
to be adapted.
The functions
)
to be adapted.
The functions
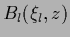 are often chosen to depend on one-dimensional
combinations of the vectors
are often chosen to depend on one-dimensional
combinations of the vectors 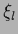 and
and 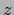 .
For example they may depend on some distance
.
For example they may depend on some distance
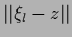 (`local or distance approaches')
or the projection of
(`local or distance approaches')
or the projection of 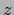 in
in 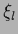 -direction, i.e.,
-direction, i.e.,
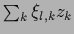 (`projection approaches').
(For projection approaches see also Sections
4.5, 4.8 and 4.9).
(`projection approaches').
(For projection approaches see also Sections
4.5, 4.8 and 4.9).
A typical example are Radial Basis Functions (RBF)
using Gaussian 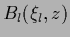 for which centers
(and possibly covariances and also number of components)
can be adjusted.
Other local methods include
for which centers
(and possibly covariances and also number of components)
can be adjusted.
Other local methods include
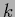 -nearest neighbors methods (
-nearest neighbors methods (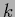 NN)
and learning vector quantizations (LVQ)
and its variants.
(For a comparison see [158].)
NN)
and learning vector quantizations (LVQ)
and its variants.
(For a comparison see [158].)
Joerg_Lemm
2001-01-21
![]() can be approximated by a mixture model,
i.e., by a linear combination of components functions
can be approximated by a mixture model,
i.e., by a linear combination of components functions
![]() for which centers
(and possibly covariances and also number of components)
can be adjusted.
Other local methods include
for which centers
(and possibly covariances and also number of components)
can be adjusted.
Other local methods include
![]() -nearest neighbors methods (
-nearest neighbors methods (![]() NN)
and learning vector quantizations (LVQ)
and its variants.
(For a comparison see [158].)
NN)
and learning vector quantizations (LVQ)
and its variants.
(For a comparison see [158].)