



Next: Mixture models
Up: Parameterizing likelihoods: Variational methods
Previous: Gaussian priors for parameters
Contents
Solving a density estimation problem numerically,
the function  has to be discretized.
This is done by expanding
has to be discretized.
This is done by expanding  in a basis
in a basis
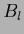 (not necessarily orthonormal)
and,
choosing some
(not necessarily orthonormal)
and,
choosing some 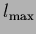 ,
truncating the sum to terms with
,
truncating the sum to terms with
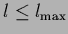 ,
,
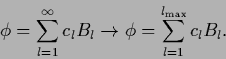 |
(380) |
This, also called Ritz's method, corresponds
to a finite linear trial space
and is equivalent
to solving a projected stationarity equation.
Using a discretization (380)
the functional (187)
becomes
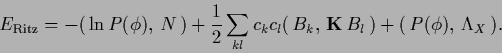 |
(381) |
Solving for the coefficients 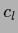 ,
,
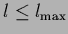 to minimize the error results
according to Eq.[355) and
to minimize the error results
according to Eq.[355) and
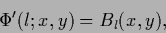 |
(382) |
in
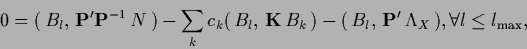 |
(383) |
corresponding to the 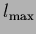 -dimensional equation
-dimensional equation
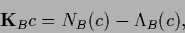 |
(384) |
with
Thus, for an orthonormal basis 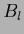 Eq. (384) corresponds
to Eq. (189) projected into the trial space
by the projector
Eq. (384) corresponds
to Eq. (189) projected into the trial space
by the projector
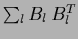 .
.
The so called linear models are obtained by the
(very restrictive) choice
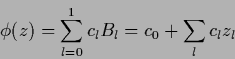 |
(389) |
with 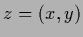 and
and
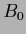 = 1 and
= 1 and 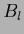 =
= 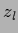 .
Interactions, i.e., terms proportional to
products of
.
Interactions, i.e., terms proportional to
products of 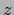 -components like
-components like 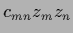 can be included.
Including all possible interaction would correspond to a
multidimensional Taylor expansion
of the function
can be included.
Including all possible interaction would correspond to a
multidimensional Taylor expansion
of the function 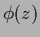 .
.
If the functions 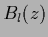 are also parameterized
this leads to mixture models for
are also parameterized
this leads to mixture models for  .
(See Section 4.4.)
.
(See Section 4.4.)




Next: Mixture models
Up: Parameterizing likelihoods: Variational methods
Previous: Gaussian priors for parameters
Contents
Joerg_Lemm
2001-01-21
![]() has to be discretized.
This is done by expanding
has to be discretized.
This is done by expanding ![]() in a basis
in a basis
![]() (not necessarily orthonormal)
and,
choosing some
(not necessarily orthonormal)
and,
choosing some ![]() ,
truncating the sum to terms with
,
truncating the sum to terms with
![]() ,
,
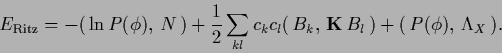
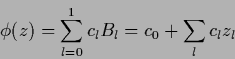
![]() are also parameterized
this leads to mixture models for
are also parameterized
this leads to mixture models for ![]() .
(See Section 4.4.)
.
(See Section 4.4.)