



Next: Example: Square root of
Up: General Gaussian prior factors
Previous: General Gaussian prior factors
Contents
The general case
In the previous sections we studied
priors consisting of a factor (the specific prior) which was Gaussian
with respect to 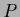 or
or 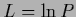 and additional normalization (and non-negativity) conditions.
In this section we consider the situation where the
probability
and additional normalization (and non-negativity) conditions.
In this section we consider the situation where the
probability  is expressed in terms of a function
is expressed in terms of a function 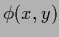 .
That means, we assume
a, possibly non-linear, operator
.
That means, we assume
a, possibly non-linear, operator
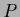 =
= 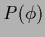 which maps the function
which maps the function  to a probability.
We can then formulate a learning problem in terms
of the function
to a probability.
We can then formulate a learning problem in terms
of the function  , meaning that
, meaning that
 now represents the hidden variables
or unknown state of Nature
now represents the hidden variables
or unknown state of Nature 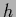 .3Consider the case of a specific prior
which is Gaussian in
.3Consider the case of a specific prior
which is Gaussian in  ,
i.e., which has a specific prior energy quadratic in
,
i.e., which has a specific prior energy quadratic in 
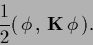 |
(186) |
This means we are lead to error functionals of the form
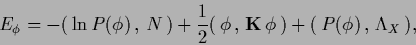 |
(187) |
where we have skipped the  -independent part of the
-independent part of the 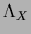 -terms.
In general cases also
the non-negativity constraint has to be implemented.
-terms.
In general cases also
the non-negativity constraint has to be implemented.
To express
the functional derivative of functional (187)
with respect to  we define
besides the diagonal matrix
we define
besides the diagonal matrix 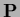 =
= 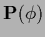 the Jacobian, i.e., the matrix of derivatives
the Jacobian, i.e., the matrix of derivatives
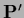 =
=
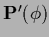 with matrix elements
with matrix elements
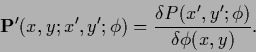 |
(188) |
The matrix
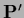 is diagonal
for point-wise transformations, i.e., for
is diagonal
for point-wise transformations, i.e., for
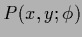 =
=
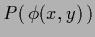 .
In such cases we use
.
In such cases we use 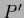 to denote the vector of diagonal elements
of
to denote the vector of diagonal elements
of
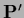 .
An example is the previously discussed transformation
.
An example is the previously discussed transformation 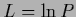 for which
for which
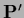 =
= 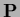 .
The stationarity equation for functional (187) becomes
.
The stationarity equation for functional (187) becomes
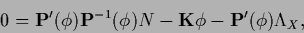 |
(189) |
and for existing
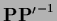 =
=
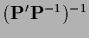 (for nonexisting inverse
see Section 4.1),
(for nonexisting inverse
see Section 4.1),
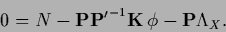 |
(190) |
From Eq. (190)
the Lagrange multiplier function can be found by integration,
using the normalization condition
 =
= 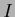 ,
in the form
,
in the form
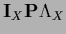 =
= 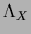 for
for
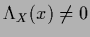 .
Thus, multiplying Eq. (190) by
.
Thus, multiplying Eq. (190) by 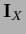 yields
yields
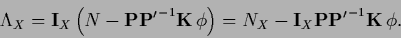 |
(191) |
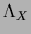 is now eliminated by
inserting Eq. (191) into Eq. (190)
is now eliminated by
inserting Eq. (191) into Eq. (190)
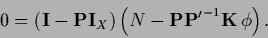 |
(192) |
A simple iteration procedure,
provided
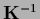 exists,
is suggested by writing
Eq. (189) in the form
exists,
is suggested by writing
Eq. (189) in the form
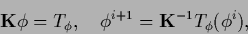 |
(193) |
with
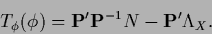 |
(194) |
Table 2
lists constraints to be implemented explicitly
for some choices of  .
.
Table 2:
Constraints for specific choices of 
 |
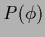 |
constraints |
 |
 |
norm |
non-negativity |
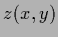 |
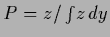 |
-- |
non-negativity |
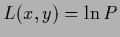 |
 |
norm |
-- |
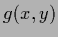 |
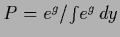 |
-- |
-- |
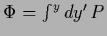 |
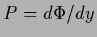 |
boundary |
monotony |
|




Next: Example: Square root of
Up: General Gaussian prior factors
Previous: General Gaussian prior factors
Contents
Joerg_Lemm
2001-01-21
![]() or
or ![]() and additional normalization (and non-negativity) conditions.
In this section we consider the situation where the
probability
and additional normalization (and non-negativity) conditions.
In this section we consider the situation where the
probability ![]() is expressed in terms of a function
is expressed in terms of a function ![]() .
That means, we assume
a, possibly non-linear, operator
.
That means, we assume
a, possibly non-linear, operator
![]() =
= ![]() which maps the function
which maps the function ![]() to a probability.
We can then formulate a learning problem in terms
of the function
to a probability.
We can then formulate a learning problem in terms
of the function ![]() , meaning that
, meaning that
![]() now represents the hidden variables
or unknown state of Nature
now represents the hidden variables
or unknown state of Nature ![]() .3Consider the case of a specific prior
which is Gaussian in
.3Consider the case of a specific prior
which is Gaussian in ![]() ,
i.e., which has a specific prior energy quadratic in
,
i.e., which has a specific prior energy quadratic in ![]()
![]() we define
besides the diagonal matrix
we define
besides the diagonal matrix ![]() =
= ![]() the Jacobian, i.e., the matrix of derivatives
the Jacobian, i.e., the matrix of derivatives
![]() =
=
![]() with matrix elements
with matrix elements
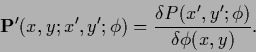
![]() .
.