



Next: Neural networks
Up: Parameterizing likelihoods: Variational methods
Previous: Decision trees
Contents
Projection pursuit
Projection pursuit models
[60,102,50]
are a generalization of additive models
(391)
(and a special case of models (393) additive in parameters)
where the projections of 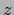 =
= 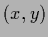 are also adapted
are also adapted
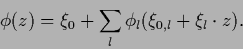 |
(408) |
For such a model one has to determine
one-dimensional `ridge' functions 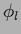 together with
projections defined by vectors
together with
projections defined by vectors 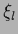 and constants
and constants 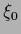 ,
, 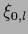 .
Adaptive projections may also be used for product approaches
.
Adaptive projections may also be used for product approaches
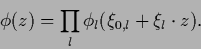 |
(409) |
Similarly,  may be decomposed into functions depending
on distances to adapted reference points (centers).
That gives models of the form
may be decomposed into functions depending
on distances to adapted reference points (centers).
That gives models of the form
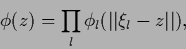 |
(410) |
which require to adapt
parameter vectors (centers) 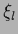 and distance functions
and distance functions 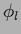 .
For high dimensional spaces
the number of centers necessary
to cover a high dimensional space
with fixed density grows exponentially.
Furthermore, as the volume of a
high dimensional sphere tends to be concentrated near its surface,
the tails become more important in higher dimensions.
Thus, typically, projection methods are better suited for
high dimensional spaces than distance methods
[211].
.
For high dimensional spaces
the number of centers necessary
to cover a high dimensional space
with fixed density grows exponentially.
Furthermore, as the volume of a
high dimensional sphere tends to be concentrated near its surface,
the tails become more important in higher dimensions.
Thus, typically, projection methods are better suited for
high dimensional spaces than distance methods
[211].




Next: Neural networks
Up: Parameterizing likelihoods: Variational methods
Previous: Decision trees
Contents
Joerg_Lemm
2001-01-21
![]() =
= ![]() are also adapted
are also adapted