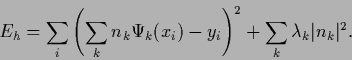Next: Classification
Up: Regression
Previous: Gaussian mixture regression (cluster
Contents
Expanding the regression function 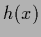 in a basis of
eigenfunctions
in a basis of
eigenfunctions 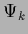 of
of 
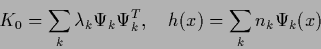 |
(333) |
yields for functional (247)
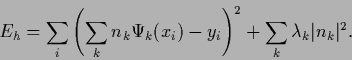 |
(334) |
Under the assumption of output noise for training data
the data terms may for example be replaced by the logarithm
of a mixture of Gaussians.
Such mixture functions with varying mean can develop flat regions
where the error is insensitive (robust) to changes of 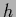 .
Analogously, Gaussians with varying mean can be added
to obtain errors which are flat compared to Gaussians for large
absolute errors.
Similarly to such Gaussian mixtures
the mean-square error data term
.
Analogously, Gaussians with varying mean can be added
to obtain errors which are flat compared to Gaussians for large
absolute errors.
Similarly to such Gaussian mixtures
the mean-square error data term
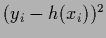 may be replaced
by an
may be replaced
by an 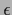 -insensitive error
-insensitive error
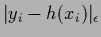 ,
which is zero for absolute errors smaller
,
which is zero for absolute errors smaller 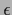 and linear
for larger absolute errors (see Fig.5).
This results in a quadratic programming problem
and is equivalent to Vapnik's support vector machine
[225,74,226,214,215,49].
For a more detailed discussion
of the relation between support vector machines
and Gaussian processes see
[229,208].
and linear
for larger absolute errors (see Fig.5).
This results in a quadratic programming problem
and is equivalent to Vapnik's support vector machine
[225,74,226,214,215,49].
For a more detailed discussion
of the relation between support vector machines
and Gaussian processes see
[229,208].
Figure 5:
Three
robust error functions which are
insensitive to small errors.
Left: Logarithm of mixture with two Gaussians with equal variance
and different means.
Middle: Logarithm of mixture with 11 Gaussians with equal variance
and different means.
Right: 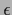 -insensitive error.
-insensitive error.
 |




Next: Classification
Up: Regression
Previous: Gaussian mixture regression (cluster
Contents
Joerg_Lemm
2001-01-21
![]() in a basis of
eigenfunctions
in a basis of
eigenfunctions ![]() of
of ![]()