Next: Support vector machines and
Up: Regression
Previous: Exact predictive density
Contents
Generalizing Gaussian regression
the likelihoods may be modeled by a mixture of  Gaussians
Gaussians
 |
(331) |
where the normalization factor is found as
 .
Hence,
.
Hence, 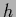 is here specified by mixing coefficients
is here specified by mixing coefficients 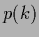 and a vector of regression functions
and a vector of regression functions
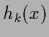 specifying the
specifying the  -dependent location of the
-dependent location of the 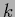 th cluster centroid
of the mixture model.
A simple prior for
th cluster centroid
of the mixture model.
A simple prior for 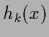 is a smoothness prior diagonal in the cluster components.
As any density
is a smoothness prior diagonal in the cluster components.
As any density  can be approximated arbitrarily
well by a mixture with large enough
can be approximated arbitrarily
well by a mixture with large enough 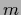 such cluster regression models
allows to interpolate between Gaussian regression
and more flexible density estimation.
such cluster regression models
allows to interpolate between Gaussian regression
and more flexible density estimation.
The posterior density becomes for independent data
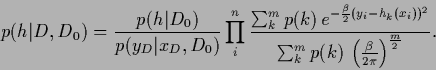 |
(332) |
Maximizing that posterior is
-- for fixed  , uniform
, uniform 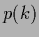 and
and 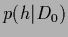 --
equivalent to the clustering approach
of Rose, Gurewitz, and Fox
for squared distance costs [203].
--
equivalent to the clustering approach
of Rose, Gurewitz, and Fox
for squared distance costs [203].




Next: Support vector machines and
Up: Regression
Previous: Exact predictive density
Contents
Joerg_Lemm
2001-01-21
![]() Gaussians
Gaussians
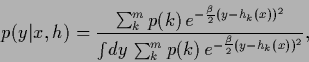
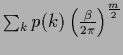 .
Hence,
.
Hence,