Seminar on the theory of particles and fields

Contents & literature

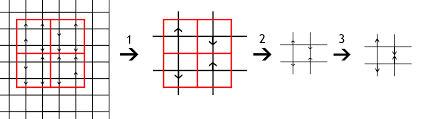
Critical phenomena are continuous phase transitions and their accompanying phenomena. They are based on a collective interaction of a (infinitely) large number of degrees of freedom and play an important role both in elementary particle theory and in statistical physics. The planned talk topics include the classical theories for the description of phase transitions as well as one of the most studied model systems, the Ising model. A successful tool for understanding critical phenomena is also provided by the renormalization group that is covered too. Its basic idea is to combine strongly correlated degrees of freedom to a common mean value, which then is understood as a new (effective) degree of freedom.

Topics are primarily given out to master’s students. A limited number of topics can possibly also be worked on by bachelor’s students. Thus, we refer to the seminar on the theory of atoms, nuclei and condensed matter at this point, which is targeted exclusively towards bachelor’s students.

Literature

• H.E. Stanley: Introduction to Phase Transitions and Critical Phenomena, Oxford University Press, 1971
• J.J. Binney, N.J. Dowrick, A.J. Fisher, M.E.J. Newman: The Theory of Critical Phenomena, Clarendon Press, 1992
• W. Gebhard, U. Krey: Phasenübergänge und kritische Phänomene, Vieweg, 1980
• W. Nolting: Grundkurs Theoretische Physik, Bände 4 & 6, Springer, 2005 & 2007
• L.D. Landau, E.M. Lifschitz: Statistische Physik, Akademie-Verlag, 1970
• H. Römer, T. Filk: Statistische Mechanik, Wiley-VCH, 1994
• W. Weidlich: Thermodynamik und statistische Mechanik, Akademische Verlagsgesellschaft, 1976
• K. Huang: Statistical Mechanics, John Wiley and Sons, 1987
• P. Pfeuty, G. Toulouse: Introduction to the Renormalization Group and to Critical Phenomena, John Wiley and Sons, 1977
• K.G. Wilson: Die Renormierungsgruppe, Spektrum der Wissenschaft 10/1979
• M.E.J. Newman, G.T. Barkema: Monte Carlo Methods in Statistical Physics, Oxford University Press, 1999
• D.P. Landau, K. Binder: A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, 2000

The literature is made available to the speakers. Further advice concerning complementary literature is given as part of the talk guidance.