In a first test we checked the initial value method for accuracy. We solved the forward problem (1.1) for the function
and k = 50 analytically and compared the exact solution with the approximate solution of the initial value method for h = 32. We found satisfactory agreement.
In a second test we used the exact data for (4.1) and k = 50 as input to our reconstruction method with p = 25, q = 32. As initial approximation we chose (4.1) with 0.2 replaced by 0.1. After 3 sweeps of our algorithm we obtained a reconstruction very similar to a low pass filtered version of f with cut off 50.
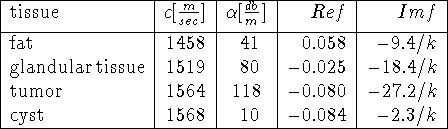
Finally we created a 3D breastphantom, see Fig. 1. It consists of fat, glandular tissue, a tumor and a cyst. The breast is suspended in a cube of sidelength 12 cm which is filled with water. f is given by
with 
m sec 
the speed of sound in water. The values of c and 
(at 1MHz) are
Since the top face of the cube is not accessible, we have to modify the finite difference method (3.1). We stipulate the boundary condition 
on the top face of 
, i.e. we let n run from -q to q and put 
. The boundary value problem (2.5) for z has to be changed accordingly. Of course this procedure is questionable, but at the present state of our work we just don't know anything better.
We generated data for p = 32 equally spaced directions in 
using our initial value method with q = 32, i.e. h = 6cm/32 = 1.875mm. The frequency of the iradiating waves was chosen to be 250 KHz, i.e. k = 10.47cm . This corresponds to a wavelength of 6mm. After three sweeps of our algorithm we obtained a reconstruction in which the cyst and the tumor where
clearly visible and distinguishable. The computing time per sweep on a
SPARC 20 was 10 minutes.
