Let 
be the cube circumscribed to the reconstruction region 
with edges parallel to the coordinate axes and aligned with the direction 
of the j-th incoming wave. Let 
be the face lying in the plane 
, and let 
be the other faces of . Rather than working with the scattered fields 
we use the scaled scattered fields 
which satisfy
Note that we do not make the parabolic approximation [8], i.e. we do not assume that the second derivative of 
in direction 
is small compared to 
.
In [12] we haved analysed the stability of the initial value problem
for this elliptic differential equation. Let
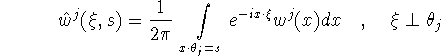
be the 2D Fourier transform of w in the plane 
. We found that 
depends in a perfectly stable way on the initial values for on 
for all frequencies 
where 
is some number depending
essentially on k and, to a minor extent, on f. In ultrasound tomography we can choose slightly smaller than k, typically 
.
Thus we may define a nonlinear map 
by
putting
The inverse scattering problem now calls for the solution of the nonlinear system
As in [12] this is done by an ART-type procedure. Starting out from an initial approximation 
, we put 
and for 
The first approximation 
is then defined to be 
. For 
we simply take the operator 
where 
is chosen such that, in the limit 
,
, i.e. 
[10]. The
evaluation of 
for some 
can be done as follows: Solve the initial value problem
Then,
where is the solution of (2.1) - (2.2). Of course the stability properties of (2.5) are exactly as discussed above.
