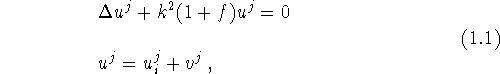
We consider the inverse problem for the 3D Helmholtz equation
where 
, 
are the incoming waves, 
satisfies the
Sommerfeld radiation condition and the function f vanishes outside the ball
of radius 
. We want to recover f numerically from knowing 
on the sphere of radius for and a fixed frequency k.
This is a model for ultrasonic tomography [6]. However we point out that in a real ultrasonic scanner the irradiating waves are no longer plane waves but standing waves in a finite container.
We start with a short survey on the extensive literature on numerical methods. With the exception of methods which use the Born or Rytov approximation [4], it seems that the only method which actually has been tested numerically in 3D is the Newton method combined with a finite Fourier expansion of f [5]. The other methods have been used in 2D only, even though an extension to 3D is possible in principle. The dual space method [2] reduces the problem from the whole space 
with the far field (which we do not use) as data to an overposed boundary value problem in a finite volume which in turn is solved by optimization.
Of course we can always try to compute the Born series [3]. For this purpose we write (1.1) as an integral equation
Here, G is the Green's function of 
with the radiation condition at 
.
The Born series 
is now obtained by solving
for 
, where 
and
with 
function satisfying the radiation condition.
The generalized SOR-method of [7] also starts out from the integral equation (1.2). Writing for the integral operator in (1.2) simply G, this method minimizes the functional
with some weight factor 
. The minimization is done by
where 
, 
are update directions and 
, 
are chosen so as to minimize (1.3).
A non iterative method has been suggested in [15]. With 
the Green's function of 
, we can rewrite (1.1) as
Now form a linear combination of the incoming waves such that the resulting field peaks at z, i.e.
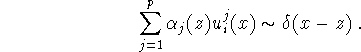
Then, from (1.4),
is approximately known on 
. From the identity
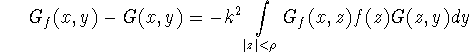
we get an approximation to 
for which together with (1.5) determines f. The method still has to be tested.
A very efficient code has been given in [6]. It is very similar to ours in that it uses initial value techniques and ignores in the Jacobian entries which correspond to different incoming waves. The initial value technique is based on factoring the Helmholtz equation into a product of two first order differential operators.
The purpose of this note is to extend the method of [14] to 3D and to conduct 3D numerical experiments. We illuminate the object by plane waves 
where the unit vectors 
are lying in a plane. We use an initial value technique as in [6], but we do not rely on parabolic approximations [8] of the Helmholtz equation.
