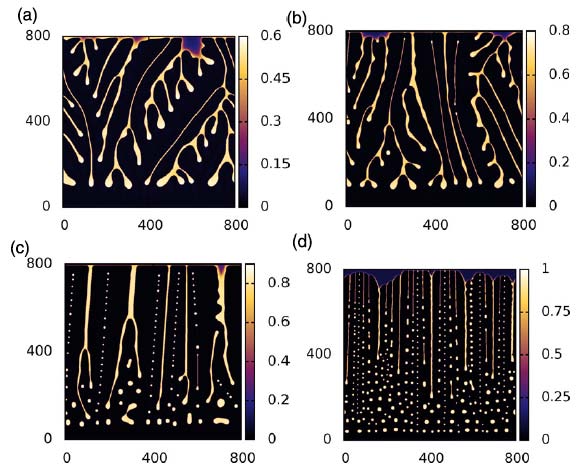
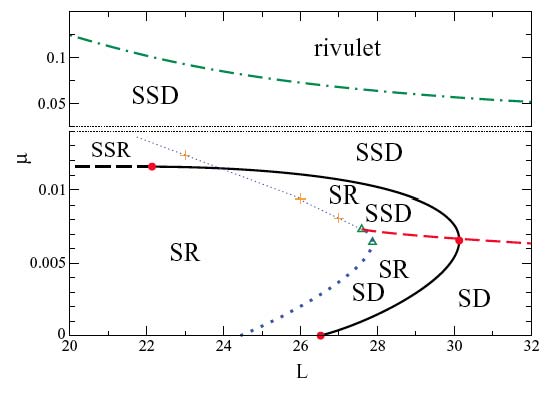
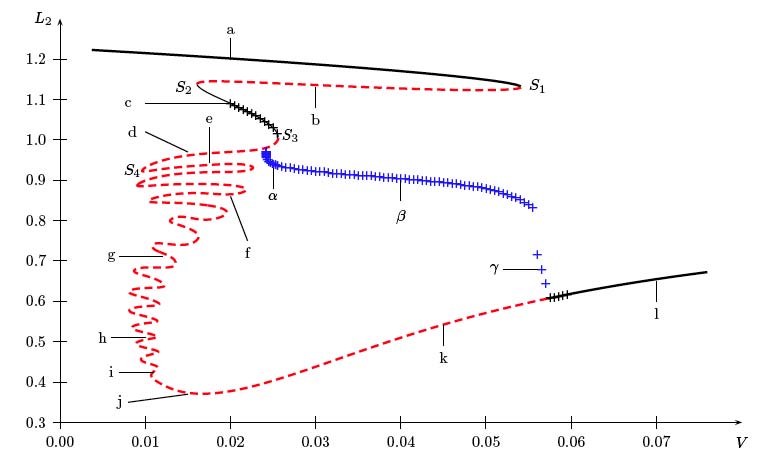
Main scientific interestMy present main interest is the interface-dominated dynamics of complex liquids and soft matter, i.e., the influence of capillarity, wettability and/or internal structural forces on dynamical processes like, dewetting, deposition, crystallisation, phase separation, etc.. This includes active (biologically inspired) media.Examples are (driven) droplets on homogeneous and heterogeneous substrates; surface-active substances, e.g., in Langmuir-Blodgett transfer; (active) liquid crystals; colloidal (nano)particle suspensions and polymer solutions; self-propelled droplets; multilayer fluid systems; crystallisation of passive and active colloidal particles and their mixtures; the dynamics of phase transitions; ratchet-driven transport in nano- and micro-fluidic systems; dynamics of wetting transitions of binary and ternary systems; Further interests are related to pattern formation in Bose-Einstein condensates and the extraction of models from data. An important objective is to understand the structure forming interaction of the various interdependent advective and diffusive transport processes, phase transitions and possibly chemical reactions. On this basis one may successfully control the pertinent experimental systems and technological applications from coating and printing processes to bottom-up nanostructuring and micro- (and nano-)fluidics. The various systems are investigated employing and developing analytical and numerical tools of nonlinear science. Af particular interest is the bifurcation structure of the various models and, in general, the relation of bifurcation diagrams and phase diagrams. The systematics of the relation between the various models, their relation to gradient dynamics formulations are also of large interest.
To facilitate students to enter the field early on
(even with their Bachelor theses) we are building up the
Münsteranian Torturials - set of hands-on tutorials on nonlinear science (numerical
path-following and time-stepping methods, analytical methods - slowly
but continuously progressing)
Scientific disciplines and model typesMany of the individual systems are situated in the twilight zone between physics, biology, chemistry and the engineering sciences and are described with methods of Theoretical Physics, Chemical and Biological Physics, Applied Mathematics, including non-equilibrium and equilibrium thermodynamics and statistical physics, physico-chemical hydrodynamics, surface science and nonlinear science.The aim to understand soft matter systems on mesoscopic scales is pursued through the application, further development and analysis of a variety of microscopic stochastic discrete and microscopic and mesoscopic deterministic continuum descriptions. Examples include kinetic Monte Carlo models, Molecular Dynamics approaches, phase field and phase field crystal models, Dynamical Density Functional Theory and mesoscopic hydrodynamic models. Analytical and Computational ApproachAs the investigated effects are rather complex and the models are nonlinear, the reach of analytical approaches is limited. Analytically, one may study the linear and marginal stability of trivial steady and stationary states and of selected non-trivial ones; asymptotic methods often allow to determine the solution structure far away from the interesting transitions; and bifurcation theory allows for studies very close to some of the transitions.The analytical work is accompanied by large-scale computations performed on systems ranging from standard laptops, to graphic cards (CUDA framework), and High Performance Parallel Computing systems. Numerical algorithms we develop and employ include standard finite difference methods or exponential propagation methods for the time stepping of ODE and PDE; pseudo arclength path continuation methods to determine steady and stationary states, and time-periodic space-dependent states. We also work on micro-meso hybrid methods, e.g., by matching Molecular Dynamics / (D)DFT and mesoscopic hydrodynamics for nano-droplets on solid substrates. CollaborationsThere exist collaborations with a number of experimentally and theoretically working groups at Departments of Mathematics, Physics, Chemical and Mechanical Engineering of various institutions in Europe, North America and Asia. For examples see the publication list. |
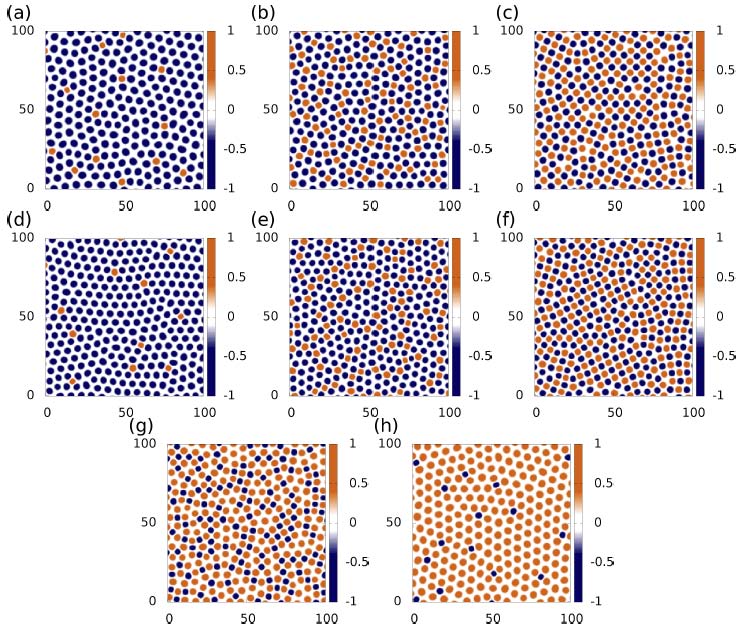
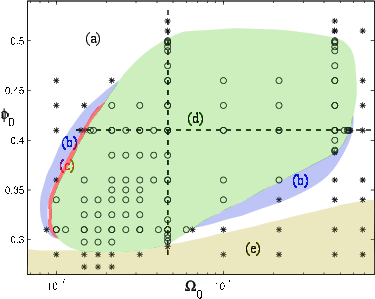
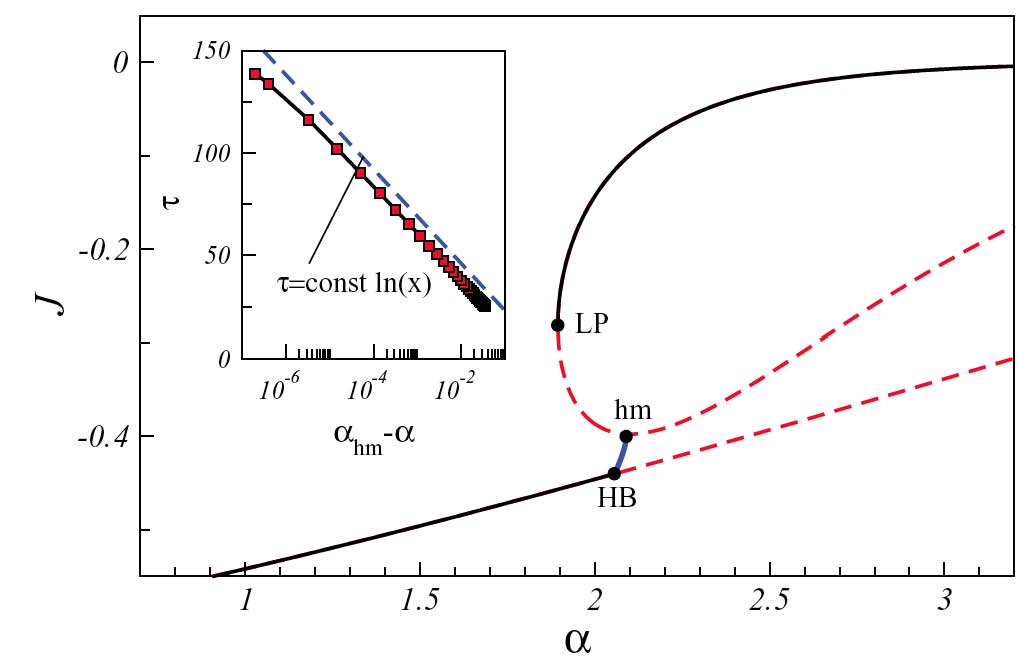
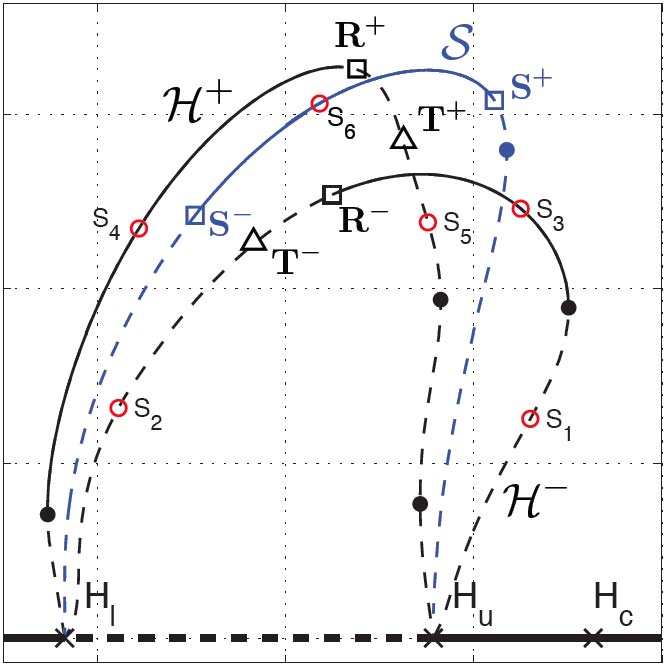
Curious patterns in a nonreciprocal Cahn-Hilliard model |
Last change:
ut 08.07.2025
Data protection policy of WWU Münster applies (see link)