



Next: Gaussian relaxation
Up: Learning matrices
Previous: Linearization and Newton algorithm
Contents
Massive relaxation
We now consider methods to construct a
positive definite or at least invertible learning matrix.
For example, far from a minimum the Hessian 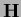 may not be positive definite
and like a differential operator
may not be positive definite
and like a differential operator 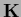 with zero modes, not even invertible.
Massive relaxation
can transform a non-invertible or not positive definite operator
with zero modes, not even invertible.
Massive relaxation
can transform a non-invertible or not positive definite operator 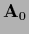 ,
e.g.
,
e.g.
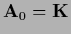 or
or
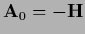 ,
into an invertible or positive definite operators:
,
into an invertible or positive definite operators:
A generalization would be to allow 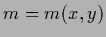 .
This is, for example, used
in some realizations of Newton`s method for minimization
in regions where
.
This is, for example, used
in some realizations of Newton`s method for minimization
in regions where 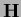 is not positive definite
and a diagonal operator is added to
is not positive definite
and a diagonal operator is added to 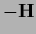 ,
using for example a modified Cholesky factorization
[19].
The mass term removes the zero modes of
,
using for example a modified Cholesky factorization
[19].
The mass term removes the zero modes of 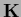 if
if 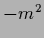 is not in the spectrum of
is not in the spectrum of 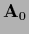 and makes it positive definite if
and makes it positive definite if 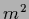 is larger than the smallest eigenvalue of
is larger than the smallest eigenvalue of 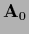 .
Matrix elements
.
Matrix elements
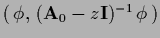 of the resolvent
of the resolvent
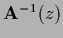 ,
,
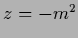 representing in this case a complex variable,
have poles at discrete eigenvalues of
representing in this case a complex variable,
have poles at discrete eigenvalues of 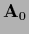 and a cut at the continuous spectrum
as long as
and a cut at the continuous spectrum
as long as 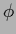 has a non-zero overlap with
the corresponding eigenfunctions.
Instead of multiples of the identity,
also other operators may be added to remove zero modes.
The Hessian
has a non-zero overlap with
the corresponding eigenfunctions.
Instead of multiples of the identity,
also other operators may be added to remove zero modes.
The Hessian 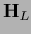 in (156), for example,
adds a
in (156), for example,
adds a 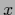 -dependent mass-like, but not necessarily positive definite
term to
-dependent mass-like, but not necessarily positive definite
term to 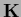 .
Similarly, for example
.
Similarly, for example 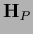 in (182) has
in (182) has
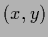 -dependent mass
-dependent mass
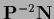 restricted to data points.
restricted to data points.
While full relaxation is the massless limit
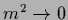 of massive
relaxation, a gradient algorithm with
of massive
relaxation, a gradient algorithm with 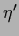 can be obtained
as infinite mass limit
can be obtained
as infinite mass limit
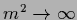 with
with
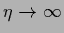 and
and
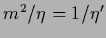 .
.
Constant functions are typical zero modes, i.e.,
eigenfunctions with zero eigenvalue,
for differential operators
with periodic boundary conditions.
For instance for a common smoothness term
 (kinetic energy operator)
as regularizing operator
(kinetic energy operator)
as regularizing operator 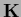 the inverse of
the inverse of
 has the form
has the form
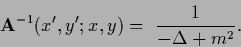 |
(639) |
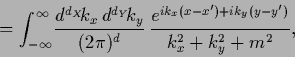 |
(640) |
with 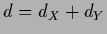 ,
, 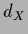 = dim(
= dim(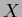 ),
), 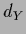 = dim(
= dim( ).
This Green`s function or matrix element of the resolvent kernel
for
).
This Green`s function or matrix element of the resolvent kernel
for 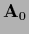 is analogous to the (Euclidean) propagator
of a free scalar field with mass
is analogous to the (Euclidean) propagator
of a free scalar field with mass 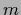 ,
which is its two-point correlation function
or matrix element of the covariance operator.
According to
,
which is its two-point correlation function
or matrix element of the covariance operator.
According to
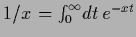 the denominator can be brought into the exponent
by introducing an additional integral.
Performing the resulting Gaussian integration over
the denominator can be brought into the exponent
by introducing an additional integral.
Performing the resulting Gaussian integration over 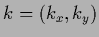 the inverse can be expressed as
the inverse can be expressed as
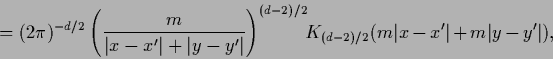 |
(641) |
in terms of the
modified Bessel functions 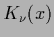 which
have the following integral representation
which
have the following integral representation
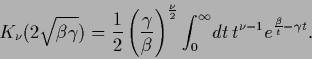 |
(642) |
Alternatively, the same result can be obtained
by switching to 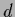 -dimensional spherical coordinates,
expanding the exponential in ultra-spheric harmonic functions
and performing the integration over the angle-variables
[117].
For the example
-dimensional spherical coordinates,
expanding the exponential in ultra-spheric harmonic functions
and performing the integration over the angle-variables
[117].
For the example  this corresponds to Parzenīs kernel
used in density estimation
or for
this corresponds to Parzenīs kernel
used in density estimation
or for 
 |
(643) |
The Green's function for periodic, Neumann, or Dirichlet boundary conditions
can be expressed by sums over
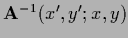 [77].
[77].
The lattice version
of the Laplacian with lattice spacing 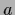 reads
reads
![\begin{displaymath}
\hat \Delta f(n) =
\frac{1}{a^2} \sum_j^d
[ f(n-a_j)-2 f(n) + f(n+a_j) ],
\end{displaymath}](img2127.png) |
(644) |
writing 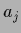 for a vector in direction
for a vector in direction 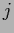 and length
and length 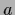 .
Including a mass term
we get as lattice approximation for
.
Including a mass term
we get as lattice approximation for 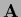
 |
(645) |
Inserting the Fourier representation (101)
of 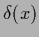 gives
gives
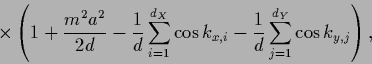 |
(646) |
with  =
= 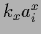 ,
, 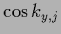 =
=
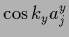 and inverse
and inverse
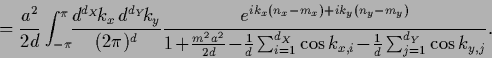 |
(647) |
(For  and
and  the integrand diverges
for
the integrand diverges
for
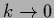 (infrared divergence).
Subtracting formally the also infinite
(infrared divergence).
Subtracting formally the also infinite
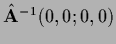 results in finite difference.
For example in
results in finite difference.
For example in  one finds
one finds
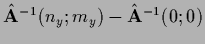 =
=
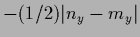 [103].
Using
[103].
Using
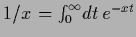 one obtains [195]
one obtains [195]
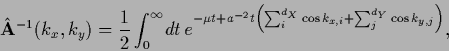 |
(648) |
with
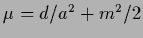 .
This allows to express the inverse
.
This allows to express the inverse
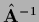 in terms of the modified Bessel functions
in terms of the modified Bessel functions 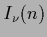 which have for integer argument
which have for integer argument 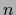 the integral representation
the integral representation
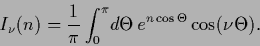 |
(649) |
One finds
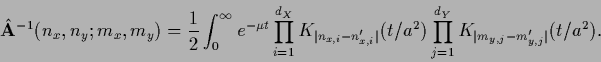 |
(650) |
It might be interesting to remark that the matrix elements of the
inverse learning matrix or free massive propagator
on the lattice
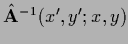 can be given an interpretation
in terms of (random) walks connecting the two points
can be given an interpretation
in terms of (random) walks connecting the two points
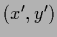 and
and 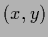 [56,195].
For that purpose
the lattice Laplacian is splitted into a diagonal and a nearest neighbor part
[56,195].
For that purpose
the lattice Laplacian is splitted into a diagonal and a nearest neighbor part
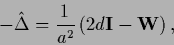 |
(651) |
where the nearest neighbor matrix
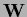 has matrix elements equal one for nearest neighbors
and equal to zero otherwise.
Thus,
has matrix elements equal one for nearest neighbors
and equal to zero otherwise.
Thus,
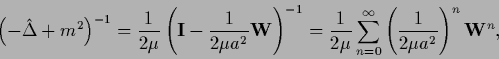 |
(652) |
can be written as geometric series.
The matrix elements
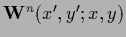 give the number of walks
give the number of walks
![$w[(x^\prime,y^\prime)\rightarrow (x,y)]$](img2156.png) of length
of length 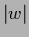 =
= 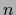 connecting
the two points
connecting
the two points
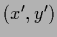 and
and 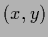 .
Thus, one can write
.
Thus, one can write
![\begin{displaymath}
\left( - \hat \Delta + m^2\right)^{-1}(x^\prime,y^\prime;x,y...
...rrow (x,y)]}
\left(\frac{1}{2 \mu a^2}\right)^{\vert w\vert} .
\end{displaymath}](img2158.png) |
(653) |




Next: Gaussian relaxation
Up: Learning matrices
Previous: Linearization and Newton algorithm
Contents
Joerg_Lemm
2001-01-21
![]() may not be positive definite
and like a differential operator
may not be positive definite
and like a differential operator ![]() with zero modes, not even invertible.
Massive relaxation
can transform a non-invertible or not positive definite operator
with zero modes, not even invertible.
Massive relaxation
can transform a non-invertible or not positive definite operator ![]() ,
e.g.
,
e.g.
![]() or
or
![]() ,
into an invertible or positive definite operators:
,
into an invertible or positive definite operators:
![]() of massive
relaxation, a gradient algorithm with
of massive
relaxation, a gradient algorithm with ![]() can be obtained
as infinite mass limit
can be obtained
as infinite mass limit
![]() with
with
![]() and
and
![]() .
.
![]() (kinetic energy operator)
as regularizing operator
(kinetic energy operator)
as regularizing operator ![]() the inverse of
the inverse of
![]() has the form
has the form
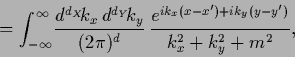
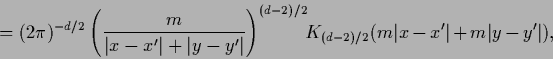

![]() [77].
[77].
![]() reads
reads
![\begin{displaymath}
\hat \Delta f(n) =
\frac{1}{a^2} \sum_j^d
[ f(n-a_j)-2 f(n) + f(n+a_j) ],
\end{displaymath}](img2127.png)


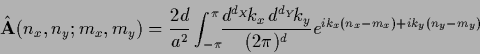
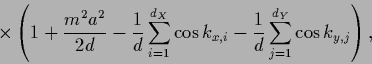

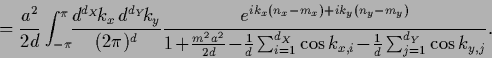
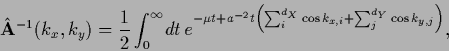
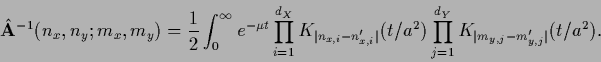
![]() can be given an interpretation
in terms of (random) walks connecting the two points
can be given an interpretation
in terms of (random) walks connecting the two points
![]() and
and ![]() [56,195].
For that purpose
the lattice Laplacian is splitted into a diagonal and a nearest neighbor part
[56,195].
For that purpose
the lattice Laplacian is splitted into a diagonal and a nearest neighbor part
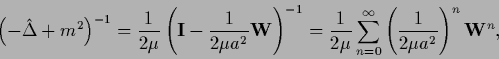
![\begin{displaymath}
\left( - \hat \Delta + m^2\right)^{-1}(x^\prime,y^\prime;x,y...
...rrow (x,y)]}
\left(\frac{1}{2 \mu a^2}\right)^{\vert w\vert} .
\end{displaymath}](img2158.png)