Next: Local masses and gauge
Up: Adapting prior covariances
Previous: General case
Contents
A useful application of hyperparameters
is the identification of sensible directions
within the space of  and
and  variables.
Consider the general case of an inverse covariance, decomposed into components
variables.
Consider the general case of an inverse covariance, decomposed into components
 =
=
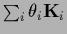 .
Treating the coefficient vector
.
Treating the coefficient vector 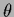 (with components
(with components  )
as hyperparameter with hyperprior
)
as hyperparameter with hyperprior 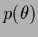 results in a prior energy (error) functional
results in a prior energy (error) functional
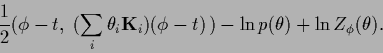 |
(463) |
The 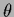 -dependent normalization
-dependent normalization
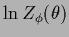 has to be included to obtain the correct
stationarity condition for
has to be included to obtain the correct
stationarity condition for 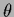 .
The components
.
The components 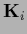 can be the components of a negative Laplacian,
for example,
can be the components of a negative Laplacian,
for example,
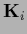 =
=
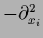 or
or
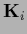 =
=
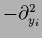 .
In that case adapting the hyperparameters
means searching for sensible directions in the
space of
.
In that case adapting the hyperparameters
means searching for sensible directions in the
space of  or
or  variables.
This technique has been called
Automatic Relevance Determination
by MacKay and Neal [170].
The positivity constraint for
variables.
This technique has been called
Automatic Relevance Determination
by MacKay and Neal [170].
The positivity constraint for 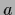 can be implemented explicitly,
for example by using
can be implemented explicitly,
for example by using
 =
=
 or
or
 =
=
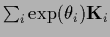 .
.
Joerg_Lemm
2001-01-21
![]() and
and ![]() variables.
Consider the general case of an inverse covariance, decomposed into components
variables.
Consider the general case of an inverse covariance, decomposed into components
![]() =
=
![]() .
Treating the coefficient vector
.
Treating the coefficient vector ![]() (with components
(with components ![]() )
as hyperparameter with hyperprior
)
as hyperparameter with hyperprior ![]() results in a prior energy (error) functional
results in a prior energy (error) functional