



Next: Automatic relevance detection
Up: Adapting prior covariances
Previous: Adapting prior covariances
Contents
Parameterizing covariances
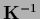 is often desirable in practice.
It includes for example adapting
the trade-off between data and prior terms
(i.e., the determination of the regularization factor),
the selection between different symmetries, smoothness measures,
or in the multidimensional situation the determination
of directions with low variance.
As far as the normalization depends on
is often desirable in practice.
It includes for example adapting
the trade-off between data and prior terms
(i.e., the determination of the regularization factor),
the selection between different symmetries, smoothness measures,
or in the multidimensional situation the determination
of directions with low variance.
As far as the normalization depends on
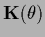 one has to consider the error functional
one has to consider the error functional
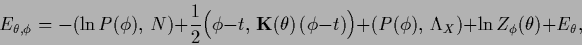 |
(456) |
with
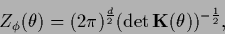 |
(457) |
for a 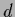 -dimensional Gaussian specific prior,
and
stationarity equations
-dimensional Gaussian specific prior,
and
stationarity equations
Here we used
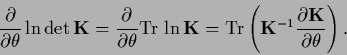 |
(460) |
In case of an unrestricted variation of the matrix elements
of 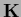 the hyperparameters become
the hyperparameters become
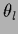 =
=
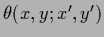 =
=
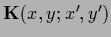 .
Then, using
.
Then, using
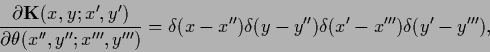 |
(461) |
Eqs.(459) becomes the inhomogeneous equation
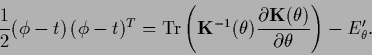 |
(462) |
We will in the sequel consider the two special cases where
the determinant of the covariance is 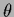 -independent
so that the trace term vanishes,
and where
-independent
so that the trace term vanishes,
and where 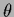 is just a multiplicative factor
for the specific prior energy, i.e., a so called regularization parameter.
is just a multiplicative factor
for the specific prior energy, i.e., a so called regularization parameter.




Next: Automatic relevance detection
Up: Adapting prior covariances
Previous: Adapting prior covariances
Contents
Joerg_Lemm
2001-01-21
![]() is often desirable in practice.
It includes for example adapting
the trade-off between data and prior terms
(i.e., the determination of the regularization factor),
the selection between different symmetries, smoothness measures,
or in the multidimensional situation the determination
of directions with low variance.
As far as the normalization depends on
is often desirable in practice.
It includes for example adapting
the trade-off between data and prior terms
(i.e., the determination of the regularization factor),
the selection between different symmetries, smoothness measures,
or in the multidimensional situation the determination
of directions with low variance.
As far as the normalization depends on
![]() one has to consider the error functional
one has to consider the error functional
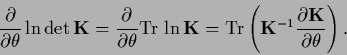
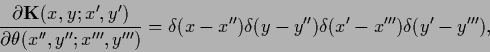
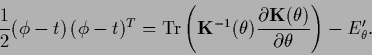
![]() -independent
so that the trace term vanishes,
and where
-independent
so that the trace term vanishes,
and where ![]() is just a multiplicative factor
for the specific prior energy, i.e., a so called regularization parameter.
is just a multiplicative factor
for the specific prior energy, i.e., a so called regularization parameter.