



Nächste Seite: Itô's Lemma
Aufwärts: Markov-Prozesse
Vorherige Seite: Langevin-Gleichung
Inhalt
Betrachten wir nun
eine allgemeine stochastische Differentialgleichung der Form,
![\begin{displaymath}
\frac{dx}{dt}
=
A[x(t),t]
+ B[x(t),t] \xi(t)
.
\end{displaymath}](img161.gif) |
(41) |
Die mathematische Bedeutung einer solchen Gleichung
ist aber nicht von vornherein klar.
Einen Schritt weiter kommen wir, wenn wir
Gl. (41)
als abkürzende Schreibweise auffassen
für die korrespondierende
Integralgleichung,
![\begin{displaymath}
x-x_0
=
\int_{t_0}^t A[x(t^\prime),t^\prime] dt^\prime
+
\int_{t_0}^t B[x(t^\prime),t^\prime] \xi(t) dt^\prime
.
\end{displaymath}](img162.gif) |
(42) |
Das mathematische Problem besteht nun darin dem
Integral
über die Zufallsvariable 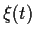 in (42)
eine Bedeutung zu geben.
In der Tat, nehmen wir an,
daß ein
in (42)
eine Bedeutung zu geben.
In der Tat, nehmen wir an,
daß ein 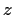 existiert mit
existiert mit
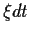 =
= 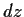 ,
also
,
also
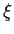 =
=
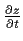 ,
wie es sein muß, damit das Integral existiert,
so finden wir beispielsweise
,
wie es sein muß, damit das Integral existiert,
so finden wir beispielsweise
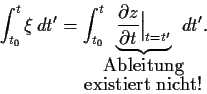 |
(43) |
Es ist aber bekannt,
daß beispielsweise bei der Brownschen Bewegung
an allen Orten die Ableitung mit Wahrscheinlichkeit 1
nicht existiert.
Damit kann das Integral im üblichen Riemann-Sinne
nicht existieren.
(Da auch die totale Variation unendlich wird,
existiert auch keine Lebesque-Integral.)
Eine Konstruktion analog zur Definition
des Riemann-Integrals als Grenzwert von Riemann-Summen
ist jedoch möglich.
Beim klassichen Riemann-Integral wird also die zu integrierende Funktion
auf äquidistanten Intervallen
 stückweise
konstant approximiert.
Das Integral über diese stückweise konstanten Funktionen
ist eine Summe, deren
Grenzwert
stückweise
konstant approximiert.
Das Integral über diese stückweise konstanten Funktionen
ist eine Summe, deren
Grenzwert
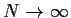 das Riemann-Integral liefert.
Anders als bei Riemann-Integralen, macht
es bei stochastischen Integralen jedoch
einen Unterschied,
an welcher Stelle des Intervalls der Funktionswert
für eine stückweise konstante Approximation gewählt wird.
Zwei Möglichkeiten sind besonders gebräuchlich.
Itô's Wahl besteht darin
stets den Funktionswert des linken Randes zu nehmen,
also
das Riemann-Integral liefert.
Anders als bei Riemann-Integralen, macht
es bei stochastischen Integralen jedoch
einen Unterschied,
an welcher Stelle des Intervalls der Funktionswert
für eine stückweise konstante Approximation gewählt wird.
Zwei Möglichkeiten sind besonders gebräuchlich.
Itô's Wahl besteht darin
stets den Funktionswert des linken Randes zu nehmen,
also
![\begin{displaymath}
\int_{t_0}^t f[x] dz
=
\lim_{N\rightarrow \infty}
\sum_{i=1}^N f[x(t_{i-1})] \Big( z(t_i) - z(t_{i-1}) \Big)
.
\end{displaymath}](img170.gif) |
(44) |
Diese Wahl korrespondiert zu der Markov-Eigenschaft.
Stratonowich wählte den Funktionwert in der Mitte
des Intervalls
![\begin{displaymath}
\int_{t_0}^t f[x] dz
=
\lim_{N\rightarrow \infty}
\sum_{i...
...t_i)+x(t_{i-1})}{2}\right] \Big( z(t_i)
- z(t_{i-1}) \Big)
.
\end{displaymath}](img171.gif) |
(45) |
Diese Wahl ist angemessen, wenn
die Diracfunktion in Gl. (36)
als Idealisierung einer
endlichen Kovarianz gesehen wird.
Für Details zur Definition stochastischer Integrale
und Differentialgleichungen sei hier beispielsweise auf
[8,1,15]
verwiesen.
Es stellt sich heraus, daß im Stratonovich-Kalkül
bezüglich Variablensubstitution in den Differentialen
die üblichen Regeln
gelten, während im Itô-Klakül
Terme zweiter Ordnung in 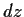 mitgenommen werden müssen.
In der Tat,
wenn
mitgenommen werden müssen.
In der Tat,
wenn 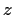 , definiert als Summe von Inkrementen
, definiert als Summe von Inkrementen 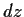 ,
eine Gauß'sche Zufallsvariable mit Mittelwert 0
und Varianz
,
eine Gauß'sche Zufallsvariable mit Mittelwert 0
und Varianz 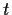 sein soll,
so muß
sein soll,
so muß 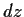 eine Gauß'sche Zufallsvariable sein mit Mittelwert 0
und Varianz
eine Gauß'sche Zufallsvariable sein mit Mittelwert 0
und Varianz 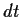 .
Dies schreibt man auch
.
Dies schreibt man auch
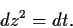 |
(46) |
Technisch gesehen, besteht der Itô-Kalkül
im wesentlichen aus der Anwendung der Beziehung (46).
Mathematisch folgt diese Beziehung aus dem Verhalten
von Itô-Integralen unter Variablensubstitution.
Sie korresondiert zu der Tatsache, daß die mittlere zurückgelegte
Weglänge
beim Wienerprozeß proportional zur Wurzel aus der Zeitdifferenz zunimmt,
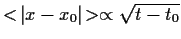 .
(Während der Erwartungswert
bei fehlendem Driftterm verschwindet,
.
(Während der Erwartungswert
bei fehlendem Driftterm verschwindet,
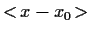 = 0.)
= 0.)
Gl. (41)
kann man nun auch mit der Variablen 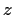 schreiben
schreiben
![\begin{displaymath}
\frac{dx}{dt}
=
A[x,t]
+ B[x,t]
\!\!\!\!\!\!\!\!\!\!
\unde...
...frac{dz}{dt}
}_{\mbox{Zufallsvariable}}
\!\!\!\!\!\!\!\!\!\!
,
\end{displaymath}](img175.gif) |
(47) |
oder, ``multipliziert'' mit 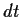 ,
in Form eines
stochastisches Differentials
,
in Form eines
stochastisches Differentials
![\begin{displaymath}
dx =
\underbrace{
A[x,t]
}_{\displaystyle \frac{\partial...
...[x,t]
}_{\displaystyle \frac{\partial x}{\partial z}}
dz
.
\end{displaymath}](img176.gif) |
(48) |
Damit erhalten wir beispielsweise
unter Verwendung von (46)
Im nächsten Abschnitt betrachten wir nun
Differentiale
von allgemeinen Funktionen ![$f[x(t),t]$](img180.gif) .
.




Nächste Seite: Itô's Lemma
Aufwärts: Markov-Prozesse
Vorherige Seite: Langevin-Gleichung
Inhalt
Joerg_Lemm
2000-02-25
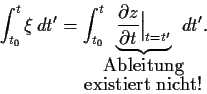
![\begin{displaymath}
\int_{t_0}^t f[x] dz
=
\lim_{N\rightarrow \infty}
\sum_{i=1}^N f[x(t_{i-1})] \Big( z(t_i) - z(t_{i-1}) \Big)
.
\end{displaymath}](img170.gif)
![\begin{displaymath}
\int_{t_0}^t f[x] dz
=
\lim_{N\rightarrow \infty}
\sum_{i...
...t_i)+x(t_{i-1})}{2}\right] \Big( z(t_i)
- z(t_{i-1}) \Big)
.
\end{displaymath}](img171.gif)
![]() schreiben
schreiben
![\begin{displaymath}
\frac{dx}{dt}
=
A[x,t]
+ B[x,t]
\!\!\!\!\!\!\!\!\!\!
\unde...
...frac{dz}{dt}
}_{\mbox{Zufallsvariable}}
\!\!\!\!\!\!\!\!\!\!
,
\end{displaymath}](img175.gif)
![\begin{displaymath}
dx =
\underbrace{
A[x,t]
}_{\displaystyle \frac{\partial...
...[x,t]
}_{\displaystyle \frac{\partial x}{\partial z}}
dz
.
\end{displaymath}](img176.gif)